- - ENERGIE CINETIQUE

On dit qu’un système possède de l’énergie quand il peut fournir du travail au milieu extérieur. L’unité de l’énergie est le joule(J).

DEFINITION

L’énergie cinétique est l’énergie que possède un corps à cause de sa vitesse.

Exemple : Un marteau lancé à grande vitesse possède de l’énergie qui permet d’enfoncer un clou.

ENERGIE CINETIQUE D’UN SOLIDE EN TRANSLATION

Un solide de masse m, se déplaçant à la vitesse v en mouvement de translation, a pour expression :

-

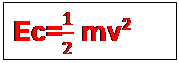
- M en kg

- V en mètre par seconde (m/s)

- Ec en joules (J)

ENERGIE CINETIQUE D’UN SOLIDE EN ROTATION

Cas d’un point matériel en rotation autour d’un axe

Soit un point matériel de masse m, en rotation autour d’un axe Δ avec une vitesse linéaire v. L’énergie cinétique de ce point est :

Ec= 1/2mv²= 1/2m(r)² =1/2 mr^{2 2}

-

-

-

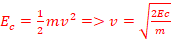
Cas d’un solide en rotation autour d’un axe Δ.

Un solide est un ensemble de points matériels m₁, m₂, m₃, ……m_i, avec i variant de 1 à n. L’énergie cinétique du solide est la somme des énergies cinétiques de tous les points matériels qui le constituent.

Ec=1/2 m₁r^{2 2} +1/2 m₂r^{2 2} + 1/2 m₃r^{2 2} +…….+ 1/2 m_ir^{2 2}

=1/2 (m₁r₁² + m₂r₂² + m₃r₃² +…….+ m_ir_i²) ²

=1/2∑m_ir_i^{2 2}

On pose J_Δ= 1/2∑m_ir_i², J_Δ est le moment d’inertie du solide S par rapport à l’axe Δ.

-

ENERGIE CINETIQUE D’UN SOLIDE DANS UN MOUVEMENT QUELCONQUE

L’énergie cinétique d’un solide s dans un mouvement combine de rotation et de translation a pour expression :

- ^-

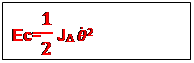
THEOREME DE L’ENERGIE CINETIQUE

Énoncé

-

La variation de l’énergie cinétique d’un système entre deux instants donnés est égale à la somme algébrique des travaux de toutes les forces agissant sur le système pendant cet intervalle de temps.

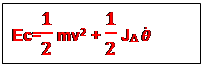
Exercice d’application

Une voiture de masse 1 t part d’un point A avec une vitesse nulle vers un point B situé à 100km avec une vitesse de 90km/h. On suppose que Les forces de frottements sont équivalentes à une force unique f=200N, opposée au sens du mouvement de la voiture. Calculer la valeur de la force motrice F de la voiture.

EXERCICES

EXERCICE I :
1.Une voiture de masse 1,25 tonne roule à la vitesse de 72 km.h^-1.
a.Calculer l’énergie cinétique qu’elle possède ?

b.Calculer cette énergie si elle roulait à 144 km.h^-1.

b.Quel est le rapport des énergies si la vitesse a doublé ?

2.Un solide de masse m=1,5t se déplace sur une route horizontale. Il possède une énergie cinétique Ec=31250J.Calculer sa vitesse.

a. En m/s

b. En km/h

EXERCICE II :

Le volant de machine à vapeur a pour moment d’inertie 12,8 kg.m^2. . Il tourne à la vitesse de rotation de 60tr/s.

1. Quelle est sa vitesse angulaire ?

2.Calculer l’énergie cinétique qu’il possède.

EXERCICE III:

Une voiture de masse 1 t part d’un point A avec une vitesse nulle vers un point B situé à 100km avec une vitesse de 90km/h. On suppose que Les forces de frottements sont équivalentes à une force unique f=200N, opposée au sens du mouvement de la voiture.

1.Calculer l’énergie cinétique en A et en B.

2. Calculer la valeur de la force motrice F de la voiture

EXERCICE IV :
Étudier le freinage d'une voiture :
Une voiture de masse m = 800 kg roule à 60 km.h^-1 sur une route horizontale. La conductrice freine et la voiture s'arrête.
1. Quelle est l'énergie cinétique initiale de la voiture?
2. Quelle est l'énergie perdue par la voiture lors de son arrêt ou quelle est la variation d’énergie cinétique
entre le début et la fin du freinage? Comment est dissipée cette énergie?

EXERCICE V:

Une platine de tourne-disque de moment d’inertie J_Δ =22x10^-3kg.m² est lancée à la vitesse de 33tr/mn. On coupe l’alimentation du moteur. La platine effectue 10 tours avant de d’arrêter.

1.Calculer les énergies cinétiques initiale et finale.

2.Calculer le moment de la force de frottement supposée constante qui s’exerce au niveau de l’axe de rotation.

EXERCICE VI : Compétence visée : Pompage de l'eau
Au cours d'une promenade en ville, deux frères découvrent un jet d'eau (propulsion de l'eau à une hauteur considérable). Émerveillés, ils se rapprochent du propriétaire de cet ouvrage pour comprendre son fonctionnement, celui-ci leur donne certaines informations contenues dans les documents A et B.
Pour un cycle de fonctionnement, la pompe propulse 498 L d'eau. Elle est alimentée par un groupe électrogène et le propriétaire estime que le coût énergique est élevé.

Document A : Caractéristiques de la pompe
• Puissance mécanique utile Pu= 830 W
• Rendement (η ) des pompes immergées η=0,79

Document B : Caractéristique du groupe électrogène
GENESIS GX 2500
• Équipement complet : 2 prises 220 V avec disjoncteur de protection et une sortie 12/24 V avec disjoncteur de protection pour la charge de la batterie
• Moteur essence 4 temps SUZUKY
• -la consommation de carburant en régime normal est de : 6 L/h
Doc C : Coût énergétique unitaire pour Données
Chaque mode d'alimentation possible
Eneo : 1kw.h coûte 79Fcfa
Groupe électrogène : 1 L d'essence
Coûte 6S0 Fcfa

Données
• Hauteur moyenne du jet : 100 mètres
• Masse volumique de l'eau : ρ = 1,0 kg/l.
• Intensité de la pesanteur : g=10 N/kg
• 1 Wh = 3600 J
En exploitant les informations ci-dessus, aidez le propriétaire à choisir le mode d’alimentation en énergie de la pompe qui permet de faire les économies

EXERCICE VII : Une société construit un barrage hydroélectrique pour alimenter une ville en énergie électrique.
Le cahier de charge demande que le barrage produise une intensité de courant minimale l=100A pour la consommation de la ville.
Le barrage est modélisé sur le schéma ci-dessous.

Le débit (volume d'eau qui fait tourner la turbine en une seconde) est de 300 m3.s1.
Le directeur s'interroge sur la capacité de la chute à faire fonctionner l'alternateur en plein régime. En plus, il se demande si le cahier de charge sera rempli.

Informations sur l'alternateur :
Fonctionnement en plein régime de l'alternateur nécessite une puissance mécanique Pm=235×106W.
Rendement η=Puissance électrique Puissance) mécanique=0,800
Tension délivrée en plein régime U=2500Kv

Information utile
L'alternateur transforme l’Energie mécanique reçue en énergie électrique.
Données : g=10,0N/kg; ρ_eau=1000kg/m³; h=78,3m.

En exploitant les informations ci-dessus et en utilisant une démarche scientifique,
1. Examine si le barrage peut faire fonctionner l'alternateur en plein régime.
2- Examine si le cahier de charge sera rempli. (PROBATOIRE D ET TI 2025)

EXERCICE VIII :

Situation problème :
Une piste de jeu de kermesse est constituée de deux parties :
• la partie AC est horizontale ;
• la partie CD de longueur 1,0 m, fait un angle α=30o avec l’’horizontale.
Pour gagner, le joueur doit loger le solide ponctuel (S) de masse m = 5,0 kg dans le réceptacle en D en partant du point A (voir figure ci-dessous).

A son tour de jeu, Ondoua, élève de première D pousse le solide (S) du point A au point B en exerçant une force constante et horizontale →F: Au point B, l'action de la force →F cesse, le solide poursuit son mouvement rectiligne sur le segment BC et arrive en C avec une vitesse de valeur
VC=3,0 m/s. Avec cette vitesse, le solide aborde le trajet CD.
Les élèves Mpito et Manga se lancent le défi d'évaluer la somme des travaux des forces qui s'exercent sur le mobile entre A et C au cours du jeu de Ondoua et sont en désaccord. Le premier a obtenu 22, 5 joules après résolution alors que le second propose 2250 joules.
Hypothèses:
• Les frottements sont négligeables ;
• Le solide part du point A sans vitesse initiale.
Données: g=10 N/kg; AB=L=4,5 m
En utilisant les informations ci-dessus et à l'aide d'une démarche scientifique :
1. Départage Mpito et Manga.
2. Examine si Ondoua est gagnant ou non. ( Probatoire D et TI 2022)

CORRIGES

EXERCICE I :
1.a-Calcul de l'énergie cinétique .

V=72x1000/3600=20m/s

Ec=1/2mv²=1/2x1250x(20)²=250000J.

b. rapport des énergies si la vitesse est doublée

Ec’==1/2x1250x(40)²=100000J

c. Rapport =1000000/250000=4. L’énergie a quadruplé lorsque la vitesse a doublé.

2.

a. =

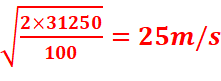
b. //1m/s =3,6km/h

EXERCICE II  :

1. Vitesse angulaire 

2.Energie cinétique qu’il possède

EXERCICE III:

1. Energie cinétique en A et en B.

=

2. Calcul de la valeur de la force motrice F de la voiture.

EXERCICE IV :

EXERCICE V:

1.Calcul des énergies cinétiques initiale et finale.

..

2.Moment de la force de frottement.

EXERCICE VI :
Il s’agit de choisir le mode d'alimentation de la pompe le plus économique. Pour ce faire pour un cycle de fonctionnement, nous allons :
• Déterminer le coût énergétique pour chaque mode d’alimentation ;
• Comparer les coûts ;
• Choisir le plus économique.
i) Détermination des coûts.
Durée T d’un cycle de fonctionnement : PuT= ρVgh⇒T =ρVghPu
Coût de l'alimentation par Enéo.
• Énergie consommée par la pompe :
C1= Wreçue=Pr.T =Puη.T =ρVghη
• Coût C₁ :
Coût de l’alimentation par le groupe
Volume Vc de carburant consommé
VC=6T(h) =6ρVghPu
Coût C2 :
C2=VC×650 ≻650 FCFA
ii) comparaison : C2≻C1, l’alimentation par Enéo est la plus économique.
L'alimentation par Enéo est celle qui permet au propriétaire de faire des économies.

EXERCICE VIII :

1. Il s'agit de déterminer la somme des travaux des forces qui s'exercent sur le mobile entre A et C afin de départager Mpito et Manga.
Pour cela, nous allons :
(i) Appliquer le théorème de l'énergie cinétique pour déterminer l'expression de la somme des travaux des forces qui s'exercent sur le mobile entre A et B ;
(ii) Appliquer le théorème de l'énergie cinétique pour déterminer l'expression de la somme des travaux des forces qui s'exercent sur le mobile entre B et C
(iii) Déduire la somme des travaux des forces qui s'exercent sur le mobile entre A et C.
(iv) Comparer la valeur obtenue aux valeurs proposées par Mpito et Manga;
(v) Conclure

• Expression de la somme des travaux des forces qui s'exercent sur le mobile entre A et B
TEC: E_CB−E_CA= ∑W_AB() avec V_A=0, Il vient que : ∑W_AB()=mv2B2
• Expression de la somme des travaux des forces qui s’exercent sur le mobile entre B et C
TEC : ECC−ECB= ∑WBC(−−→Fext)
Il Vient que : ∑WBC(−−→Fext)= mv2C2−mv2B2
• Somme des travaux des forces qui s’exercent sur le mobile entre A et C
∑WAC(−−→Fext)= ∑WAB(−−→Fext)+ ∑WBC(−−→Fext)
Il vient que : ∑WAC(−−→Fext) =mv2C2
AN : ∑WAC(−−→Fext) =22,5J
• Comparaison :
∑WAC(−−→Fext) =22,5J
• Conclusion : Mpito a raison
2. Il s'agit de déterminer la distance d parcourue par le solide sur le tronçon CD ( au moment où sa vitesse s’annule) afin de savoir si le jeu de Ondoua est gagnant ou non.
Pour cela, nous allons :
(i) Faire le bilan des forces qui s’exercent sur le solide entre C et D ;
(ii) Appliquer le TEC (ou la conservation de l’énergie mécanique) entre les points C et D pour déterminer d ,
(iii) Comparer la valeur obtenue à CD.
(v) Conclure.
• Bilan des forces Système:
solide (S)
image jeu plan incline
Forces extérieures: le poids du solide et la réaction du support.
• Application du TEC
ECf−ECC= ∑W(−−→Fext)
ECf−ECC= W(→P)+W(→R)
Or W(→R)=0, car (→R⊥−−→CD) et ECf=0 et W(→P)=−mgdsinα
soit d: d=v2C2gsinα
AN : d=0,9m
• Comparaison
d=0,9m≺CD
• Conclusion
Le jeu de Ondoua n’est pas gagnant

Avez-vous un exercice à proposer ? Cliquez-ici