APPLICATION DE L’ENERGIE CINETIQUE AUX CHOCS (COLLISIONS)

Quantité de Mouvement

Définition

La quantité de mouvement (souvent notée p) d'un objet est le produit de sa masse (m) par sa vitesse (v) :

C'est une grandeur vectorielle, donc elle a une direction et un sens.

conservation de la quantité de mouvement.

Dans un système isolé (sans forces externes), la quantité de mouvement totale avant un choc est égale à la quantité de mouvement totale après le choc.

∑ ∑

Cela signifie que même si les objets changent de vitesse individuellement, la quantité totale de 'mouvement' reste la même.

Choc mou

Un choc mou est un choc pour lequel des objets restent collés ensembles après l'impact et se déplacent avec la même vitesse finale.

La perte d'énergie cinétique est maximale dans ce type de choc.

Supposons qu’une particule de mass m₁ se déplaçant à une vitesse , heurte une cible immobile de masse m₂, puis se lie à elle. Apres la collision, Les deux se déplacent à une vitesse .

La conservation de la quantité de mouvement s’écrit :

On trouve :

Exemple : Une balle de tennis qui frappe un bloc de pâte à modeler et y reste collée. Les deux se déplacent ensemble après l'impact.

Exercice d’application 1 :

Lors du choc mou de deux corps on a les données suivantes : m₁ = 20 g ; v₁ = 160 m/s ; m₂ = 30 g. Le deuxième corps est au repos avant le choc, calculons la vitesse finale V (commune !) des 2 corps.

AVANT LE CHOC	APRES LE CHOC
p=m₁V₁ +m₂V₂	p’=(m₁+m₂)V

La conservation de la quantité de mouvement permet d’écrire : p=p’

m₁V₁ +m₂V₂=(m₁+m₂)V =>

Choc élastique

Un choc élastique est une collision où l'énergie cinétique totale du système est conservée. En d'autres termes, aucune énergie n'est perdue sous forme de chaleur, de son ou de déformation. Les billes de billard qui s'entrechoquent (en approximation) ou la collision de deux balles parfaitement rebondissantes peuvent être considérées comme des chocs élastiques.

Dans un choc élastique, deux lois de conservation s'appliquent :

Conservation de la quantité de mouvement.

Conservation de l'énergie cinétique.

Ces deux lois permettent de résoudre des problèmes impliquant des chocs élastiques et de déterminer les vitesses des objets après la collision.

Exemple : Deux boules de billard qui se percutent. Une partie de l'énergie est convertie en son, mais la majeure partie est conservée.

Exercice d’application :

Lors du choc élastique de deux corps on a les données suivantes : m₁ = 20 g ; v₁ = 160 m/s ; m₂ = 30 g. Le deuxième corps est au repos avant le choc, calculons les vitesses finales v’₁ et v’₂ des 2 corps en supposant quelles sont colinéaires.

Pour un choc élastique :

-il y a conservation de la quantité de mouvement.

+ +

- il y a conservation de la quantité de l’énergie cinétique.

+ +

On résout le système :

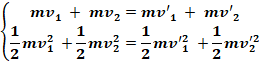
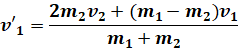
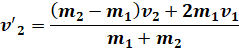
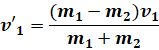
Considérons la collision élastique entre un point matériel de masse m1 anime d’une vitesse et un point matériel m₂ initialement au repos.

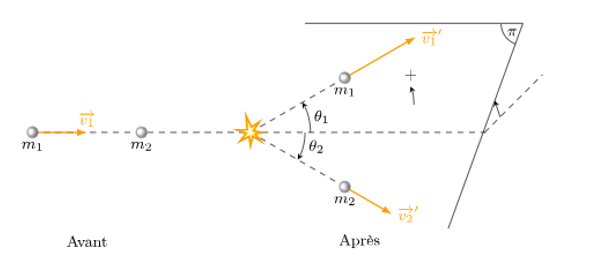
Les lois de conservation donnent :

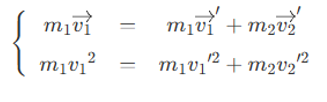
Avec :

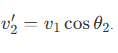
EXERCICES

EXERCICE I :

1.Une bille A de masse 0,5 kg se déplace à 4 m/s. Elle percute une bille B de masse 1 kg, initialement immobile. Après le choc, les deux billes restent collées.

Déterminer la vitesse finale commune.

2 .Une voiture A de 800 kg roule à 20 m/s et rattrape une voiture B de 600 kg roulant à 10 m/s. Après un choc mou, elles restent accrochées.

Déterminer leur vitesse commune après le choc.

3.Deux patineurs, l’un de 60 kg allant à 3 m/s vers l’est, l’autre de 80 kg à 2 m/s vers l’ouest, se percutent et restent accrochés.

Déterminer leur vitesse commune après le choc.

EXERCICE II :

1.Un chariot A (2 kg) glisse à 6 m/s sur un rail horizontal sans frottement. Il percute un autre chariot B (3 kg) initialement au repos. Après le choc, ils restent liés.

a. Déterminer la vitesse commune après le choc.

b. Calculer la perte d'énergie cinétique.

2 : Une boule A (1,5 kg) est suspendue et lâchée sans vitesse initiale depuis une hauteur de 0,8 m. Elle percute une autre boule B (2,5 kg) au repos. Après collision, les deux restent accrochées.

a. Calculer la vitesse de A juste avant le choc.

b. Trouver la vitesse commune.

c. Calculer la perte d’énergie.

3.Un bloc A (4 kg) glisse sur un plan incliné à 30°, à 5 m/s. Il rattrape un bloc B (2 kg) au repos et s’y colle.

a. Trouver la vitesse après collision.

b. Calculer la perte d’énergie.

c. Interpréter cette perte.

EXERCICE III

Une balle de masse 200 g (0,2 kg) arrive perpendiculairement à un mur avec une vitesse de 5 m/s. Après le choc, elle repart dans la direction opposée avec la même vitesse.

Questions :

a) Quelle est la variation de quantité de mouvement ?

b) Quelle est la variation d'énergie cinétique ?

EXERCICE IV :

Deux billes A et B de masses mA = mB = 0,1 kg. A arrive avec une vitesse vA = 4 m/s, B est au repos. Le choc est frontal et élastique.

Questions :

a) Quelles sont les vitesses après le choc ?

b) Vérifier la conservation de l'énergie cinétique.

EXERCICE V :

Une boule de billard (A) de 0,15 kg percute une autre (B) de même masse, initialement au repos. Après le choc, A part à 30° avec 2 m/s, B part à 60° avec 1,73 m/s.

Questions :

a) Vérifier la conservation de la quantité de mouvement.

b) Vérifier la conservation de l’énergie cinétique.

EXERCICE VI :

Une balle A de masse 0,2 kg se déplace à 6 m/s et percute une autre balle B de masse 0,3 kg immobile. Le choc est frontal et élastique.

a) Déterminer les vitesses finales de A et B.

b) Vérifier la conservation de la quantité de mouvement et de l’énergie cinétique.

EXERCICES VI :

Deux boules de masse m = 0,5 kg. La boule A arrive avec 5 m/s, la boule B est au repos.

Le choc est oblique, et après collision :

- A dévie de 60°

- B dévie de 30°

Question : Déterminer les vitesses finales vA' et vB' en supposant un choc parfaitement élastique.

EXERCICE VII :

Trois billes A, B et C (mêmes masses m = 0,1 kg) sont alignées sur un rail horizontal. A arrive à 3 m/s, B et C sont au repos. Tous les chocs sont frontalement élastiques.

Question :

Déterminer les vitesses finales après tous les chocs.

CORRIGES

EXERCICE I

1. Conservation de la quantité de mouvement :

mA·vA + mB·vB = (mA + mB)·v'

⇒ 0,5×4 + 1×0 = 1,5·v'

⇒ v' = 2 / 1,5 = 1,33 m/s

2 . Conservation de la quantité de mouvement :

800×20 + 600×10 = (800+600)·v'

⇒ 16000 + 6000 = 1400·v'

⇒ v' = 22000 / 1400 = 15,71 m/s

3 . Sens est = positif, ouest = négatif

⇒ 60×3 + 80×(–2) = (60+80)·v'

⇒ 180 – 160 = 140·v'

⇒ v' = 20 / 140 ≈ 0,14 m/s vers l’est

EXERCICE II :

a. Conservation de la quantité de mouvement :

(2×6 + 3×0) = (2+3)·v' ⇒ v' = 12 / 5 = 2,4 m/s

b. Énergie cinétique initiale :

Ec_i = ½·2·6² = 36 J

Énergie cinétique finale :

Ec_f = ½·(2+3)·(2,4)² = 0,5·5·5,76 = 14,4 J

Perte : ΔEc = 36 – 14,4 = 21,6 J

2 :

a. Conservation de l’énergie potentielle :

vA = √(2gh) = √(2×9,8×0,8) ≈ 3,96 m/s

b. Quantité de mouvement :

(1,5×3,96) = (1,5+2,5)·v' ⇒ v' = 5,94 / 4 = 1,49 m/s

[02:09, 15/12/2025] ChatGPT: 3. Ec_i = ½·1,5·(3,96)² ≈ 11,75 J

Ec_f = ½·4·(1,49)² ≈ 4,44 J

ΔEc = 7,31 J

a. v' = (4×5)/(4+2) = 20 / 6 = 3,33 m/s

b. Ec_i = ½·4·25 = 50 J

Ec_f = ½·6·(3,33)² ≈ 33,3 J

ΔEc = 16,7 J

c. Interprétation : Énergie dissipée sous forme de chaleur, déformation...

EXERCICE III :

- Avant : p₁ = 0,2 × 5 = 1 kg·m/s

- Après : p₂ = 0,2 × (-5) = -1 kg·m/s

- Δp = p₂ - p₁ = -1 - 1 = -2 kg·m/s

Énergie cinétique conservée :

- E₁ = ½ × 0,2 × 5² = 2,5 J

- E₂ = 2,5 J → ΔE = 0 J

EXERCICE IV :

a)Dans un choc élastique entre 2 objets de même masse, si l’un est au repos :

- A s’arrête : vA’ = 0 m/s

- B prend la vitesse de A : vB’ = 4 m/s

- E avant = ½ × 0,1 × 4² = 0,8 J

- E après = ½ × 0,1 × 4² = 0,8 J → OK

EXERCICE V :

a) Décomposer les vitesses en x et y, puis vérifier ∑p_x et ∑p_y avant = après.

- E₁ = ½ × 0,15 × v₁² = ½ × 0,15 × (3)² = 0,675 J

- E après = ½ × 0,15 × 2² + ½ × 0,15 × 1,73² ≈ 0,675 J → OK

EXERCICES VI :

- de la quantité de mouvement vectorielle (x et y)

- de l’énergie cinétique

Système :

- p_x : m v = m vA' cos(60°) + m vB' cos(30°)

- p_y : 0 = m vA' sin(60°) - m vB' sin(30°)

- E : ½ m v² = ½ m vA'² + ½ m vB'²

Résolution (valeurs numériques après simplifications) →

vA' = 2.5 m/s, vB' = 4.33 m/s

EXERCICE VII :

1. A percute B (mêmes masses) :

- A → 0 m/s, B → 3 m/s

2. B percute C (mêmes masses) :

- B → 0 m/s, C → 3 m/s

⇒ Résultat final :

A : 0 m/s, B : 0 m/s, C : 3 m/s