MOUVEMENT D'UNE
PARTICULE DANS UN CHAMP ELECTRIQUE
Accélération d’une particule chargée dans un champ électrostatique
uniforme
Une particule chargée de masse m et de
charge électrique q dans un champ électrostatique ![]() et se trouvant également dans le
champ de pesanteur
et se trouvant également dans le
champ de pesanteur ![]() subit deux forces :
subit deux forces :
• la force électrique ![]()
• son poids ![]()
On
admettra que l’ensemble des forces appliquées à la particule se réduit à la
force électrostatique car le poids est négligeable. Le mouvement de la
particule est assimilable à celui de son centre d’inertie.
D’après le TCI :
![]()
Le vecteur accélération
d’une particule chargée dans un champ électrostatique uniforme est un vecteur
constant, de même direction que la force électrique qu’elle subit.
• si q >
0, ![]() est de même sens que
est de même sens que ![]()
• si q <
0, ![]() est de sens contraire à
est de sens contraire à ![]()
Déviation d’une particule
La figure ci-dessous décrit la déviation d’un faisceau d’ions négatifs
pénétrant dans un champ électrostatique uniforme avec une vitesse initiale ![]() perpendiculaire au champ
perpendiculaire au champ ![]() .
.
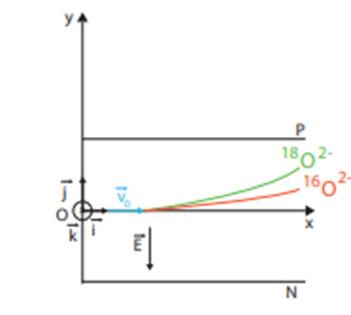
Comme la tension UPN
est positive car la plaque P est positive et la plaque N négative, les
ions négatifs sont déviés en direction de l’armature P. S’il s’agissait de
particules chargées positivement, la déviation serait de sens contraire.
Equation
horaire du mouvement
Dans le référentiel de laboratoire, la position du centre d’inertie est
étudiée dans le repère ![]() défini tel que
l’origine O coïncide avec la position du centre d’inertie de la particule et
l’axe vertical
défini tel que
l’origine O coïncide avec la position du centre d’inertie de la particule et
l’axe vertical ![]() est orientée
positivement vers le haut.
est orientée
positivement vers le haut.

Le vecteur vitesse
initiale étant contenu dans le plan vertical (xOy),
ses composants sont :

Les composants du
vecteur position du centre d’inertie obtenus par intégration sont :

Ces équations montrent que le mouvement de la
particule :
-est uniforme sur l’axe Ox
-est uniformément varie sur l’axe Oy
-s’effectue dans le plan xOy
contenant ![]()
Equation de la trajectoire
En éliminant le
temps entre les équations horaires x et y, on obtient l’expression :

C’est l’equation d’une
parabole.
Déflexion électrostatique
Etudions la déviation produite par les armatures d’un condensateur de
longueur l sur une particule de charge q. Pour cela, on place un écran
perpendiculaire a l’axe Ox a une distance D du milieu
des armatures.
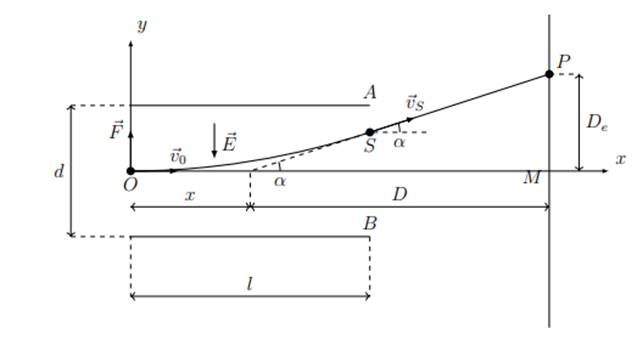
La particule sort du
condensateur au point S tel que :
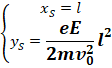
Au-delà de S,
la particule n’étant plus soumise qu’a son poids (d’ailleurs négligeable), se
comporte comme si elle était pseudo-isolé et prend un mouvement rectiligne
uniforme de vitesse ![]() .On admet que le prolongement de la tangente a la trajectoire passe au
point d’abscisse x tel que x=l/2.
.On admet que le prolongement de la tangente a la trajectoire passe au
point d’abscisse x tel que x=l/2.
Après sa sortie, la particule n’est plus soumise à la
force électrique, elle continue donc son mouvement jusqu’à son arrivée à un
point P, on remarque une distance importante De, c’est la distance qui sépare P
du point d’impact M, si ![]() était absent.
était absent.
La déviation PM
est égale à la valeur de l’ordonnée yP du point
P.
On a :
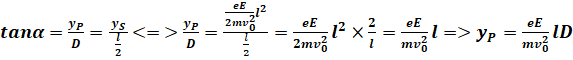
Sachant que
E=U/d
EXERCICES
EXERCICE I :
Les électrons pénètrent en O avec une vitesse v0 entre deux
plaques P et P’ distantes de d=25 cm et de longueur L=10 cm. On applique entre
les plaques une tension U créant un champ électrique uniforme de valeur E. La
déviation des protons est dirigée vers le haut. La force de la pesanteur est
négligeable.
Données : v=800
km/s ; charge d’un proton : q=1,6.10-19 C; masse
du proton : m=1,67.10-27 kg
1.Etablir l’équation
cartésienne de la trajectoire entre les plaques.
2. donner la
condition pour que le faisceau de proton sorte du champ électrique sans heurter
l’une des plaques.
3.Calculer la valeur maximale de la tension U pour que cette condition
soit réalisée
EXERCICE II :
Un faisceau d’électrons homocinétiques est émis en O a
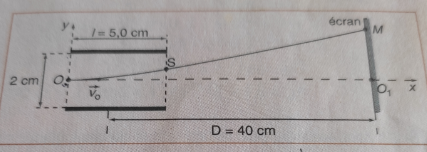
l’entrée d’un condensateur plan, avec une vitesse v0=2,0.107m/s.
il sort du condensateur au point S de coordonnées xS=50cm
et yS=0,8cm et frappe un écran fluorescent
situe à 40cm du milieu des plaques, en un point M. Les plaques du condensateur
sont distantes de 2 cm. La différence de potentiel entre les armatures du
condensateur est UAC=290V. Déterminer :
1.L’ordonnee du point
M.
2. La charge massique
de l’électron.
EXERCICE III :
Un
électron de masse m=9x10-31 kg et de charge q=-1,6x10-19 C
et un positron de même masse et de charge opposée, pénètrent avec la même
vitesse initiale horizontale de module V0 = 10 7 m/s dans
un champ électrostatique uniforme ![]() établi entre les armatures d’un
condensateur-plan. Le vecteur vitesse initiale et champ électrostatique sont
orthogonaux. Dans un repère orthonormé dont l’origine est située à l’entrée du
condensateur, l’équation cartésienne de la trajectoire de l’électron dans le
champ est de la forme :
établi entre les armatures d’un
condensateur-plan. Le vecteur vitesse initiale et champ électrostatique sont
orthogonaux. Dans un repère orthonormé dont l’origine est située à l’entrée du
condensateur, l’équation cartésienne de la trajectoire de l’électron dans le
champ est de la forme :
![]() -
- 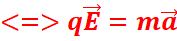
a)
Faire
un schéma montrant le condensateur, la vitesse initiale et les axes du repère
choisi.
b)
Donner,
sans calcul, l’équation cartésienne du positron.
c)
On
admet que les particules vont sortir du champ. Dans un même schéma, donner
l’allure des deux trajectoires et placer les deux points de sortie S1
et S2 à l’autre extrémité du condensateur.
d)
Calculer
la distance d=S1S2.
On donne :
U (ddp entre les
armatures du condensateur) =100V ;
L(distance entre les deux plaques) =2cm,
l (longueur du condensateur) =5cm
EXERCICE IV :
Situation
problème
L'usine « ELEC n’est
spécialisée dans la fabrication des électromètres (appareils permettant de
mesurer la charge électrique). Chaque appareil doit subir préalablement des
tests de conformité avant sa commercialisation.
Avec un électromètre neuf, le responsable effectue une mesure directe de la
charge d'une particule (S) de masse m=0,50mg;
celui-ci indique q=+1,0×10−9C. Afin de vérifier la conformité de cet
appareil, deux tests sont réalisés :
Premier test :
La particule est suspendue en un point support O par l'intermédiaire d'un fil
en soie et placée dans une région où règne un champ électrique horizontale et
uniforme →E , orienté vers la droite.
On constate que le fil s'incline d'un angle θ=11,31overs la droite.
Deuxième test:
Hypothèse : on néglige l'influence du poids.
La particule est mise en mouvement avec une vitesse →V de
valeur constante dans un champ magnétique uniforme →B tel
que →V et →B soient perpendiculaires. On
constate que le rayon de la trajectoire de la sphère est R=10,0m.

Données :
intensité de la pesanteur : g=10N/kg; E=1000V/m; B=0,050T; V=1,0rnm/s.
1. En utilisant les informations ci-dessus et à l'aide d’une démarche
scientifique, examine si le premier test est concluant ou non.
2. Exploite les résultats des tests pour te prononcer sur la commercialisation
de l’électromètre. (Baccalauréat C et E 2022)
CORRIGES :
EXERCICE
I :
1.Equation
cartésienne de la trajectoire entre les plaques.
La force extérieure
appliquée au système est ![]()
L’intensité du champ est liée à
la tension par la relation : ![]()
Le théorème du centre d’inertie
s’écrit :
![]()
![]()
![]()
A t=0 la particule est en O(xo=0,vo=0)
avec une vitesse v0(v0x=v0,v0y=0)
On a : ![]() (Ex=0,Ey=E) d’où
(Ex=0,Ey=E) d’où ![]() (ax=0, ay=qE/m)
(ax=0, ay=qE/m)
Suivant l’axe horizontale, on
a :
ax=0 => vx=cte=v0
Le mouvement est donc uniforme.
L’équation horaire du mouvement s’écrit :
x=v0t
(1)
Suivant l’axe vertical, on
a :
ay=qE/m=cte => le mouvement est
donc rectiligne uniformément varie et parallèle a E.
Les
équations horaires du mouvement sont :
![]() (2)
(2)
L’équation
cartésienne de la trajectoire entre les plaques est donnée par élimination du
temps t entre les équations paramétriques (1) et (2)
(1) => x=v0t
=> t=x/ v0
(2)
=>
![]()
2. condition pour que le faisceau de proton sorte
du champ électrique sans heurter l’une des plaques.
Lorsque la
particule est au point de sortie S, son abscisse est : x=L. La durée t1
de passage entre les plaques est alors
donnée par : x=L=v0t1 ; la déviation
parabolique de la particule a lieu pendant la durée t1=L/v0
Le point de
sortie S des plaques a :
Pour
abscisse : xS=L
Pour
ordonnée :
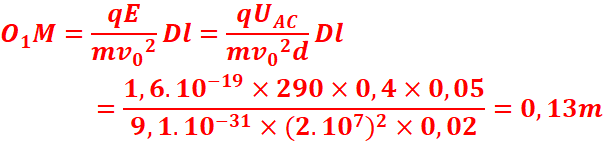
Pour
x=L ;|yS|≤d/2 =>
![]()
3. valeur maximale
de la tension U pour que cette condition soit réalisée.
![]()
EXERCICE II :
1.L’ordonnee
du point M.
L’équation
de la trajectoire est ![]()
Au-delà
de S, la particule prend un mouvement uniforme car n’étant plus soumis qu’a l’action de son poids
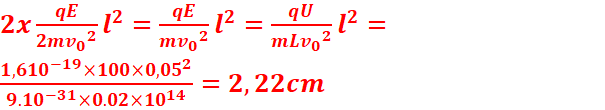
2. La
charge massique de l’électron.
xS =l
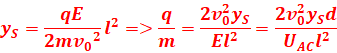
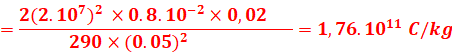
EXERCICE III :
a)
b)
Equation cartésienne du positron.
La charge du positron est positive (q=+e)
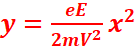
c)
d)
Calculer la distance d=S1S2.
Soit O1, le milieu de S1S2
d=2O1S1=2yS1=
![]()
EXERCICE IV :
1. Est question de vérifier la valeur de la charge
électrique q obtenue par l’électromètre
Pour cela nous allons
• Faire le bilan des forces
• Déterminer la charge de la particule
• Comparer cette valeur avec la valeur obtenue par l’électromètre et conclure
Schéma de la situation

Détermination de q

Le résultat est conforme a la mesure de l’électromètre : Le
test est concluant
2. Il est question ici de vérifier par la deuxième test la valeur de la charge
électrique q obtenue par l’électromètre
Pour cela nous allons :
• Faire le bilan des forces
• Déterminer la charge de la particule
• Comparer cette valeur avec la valeur obtenue par l’électromètre et conclure
Schéma de la situation
Détermination de g

Le résultat est conforme à la mesure de l’électromètre : L’appareil peut être
commercialise
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire