LE TRAVAIL D’UNE FORCE
NOTION DU
TRAVAIL
La
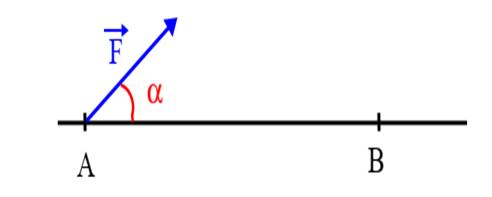
notion de travail d’une force fait intervenir deux facteurs : le facteur force
et le facteur déplacement. En général, une force travaille lorsque son point
d’application se déplace d’un endroit à un autre.
Définition
Le travail d’une force ![]() lors d’un
déplacement de son point d’application d’un point A vers un point B est égal au
produit scalaire de la force
lors d’un
déplacement de son point d’application d’un point A vers un point B est égal au
produit scalaire de la force ![]() par le
vecteur déplacement
par le
vecteur déplacement ![]() .
.
|
|
WAB() =F. AB cos =F.ABcosα Unité du
travail L’unité de travail dans le système international
est le joule(J). Le joule est donc le travail d’une force de 1N dans sa
propre direction. . W
en joules (J) F en newton(N) AB en mètre(m) |
Le travail,
grandeur algébrique
Le
travail est une grandeur algébrique. Sa valeur numérique peut être positive ou
négative.
Le travail peut être :
-Positif si 0 ≤
α< π/2 → cosα >
O le travail est dit moteur
-Négatif si π/2<α<π →
cosα < O le travail est dit résistant
-Nul si α= π/2 le travail d’une
force perpendiculaire à son déplacement est nul.
TRAVAIL D’UNE
FORCE CONSTANTE POUR UN DEPLACEMENT AB DE SON POINT D’APPLICATION
Le trajet AB peut être décomposé en de petits
déplacements rectilignes![]() ,
, ![]()
![]() ,
, ![]()
Le travail de la force ![]() , pour le déplacement
de A à B est la somme des travaux correspondants à ces petits déplacements.
, pour le déplacement
de A à B est la somme des travaux correspondants à ces petits déplacements.
WAB (![]() ) =
) =![]() +
+ ![]() .
.![]()
= ![]() (
(![]() 1 +
1 +![]() +
+![]() +….
+…. ![]() )
)
= ![]() .
.![]()
Conclusion : Le travail de la force ![]() ne dépend pas du chemin suivi entre A et B, mais seulement du point de
départ A et du point d’arrivée B.
ne dépend pas du chemin suivi entre A et B, mais seulement du point de
départ A et du point d’arrivée B.
Cas particulier du poids
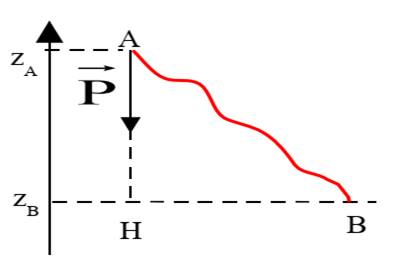
Soit
un objet de poids ![]() dont le centre de gravité de l’objet se déplace d’un point A à un point B
suivant le trajet (t). Le poids
dont le centre de gravité de l’objet se déplace d’un point A à un point B
suivant le trajet (t). Le poids ![]() de l’objet reste constant durant le déplacement.
de l’objet reste constant durant le déplacement.
|
|
WAB =F.AB cos ϴ= P.AH
= +ph Ici, le travail du poids est moteur. Lorsque l’objet monte plutôt, le travail devient WAB = F.AB
cosϴ = —ph, Il est résistant. |
Conclusion : Le
travail du poids ne dépend pas du chemin suivi, mais de la différence d’altitude
entre le point de départ et le point d’arrivée
Exercice d’application
Calculer le travail d’une force ![]() appliquée à un solide qui se déplace en mouvement rectiligne d’une
distance égale à 10m .La force
appliquée à un solide qui se déplace en mouvement rectiligne d’une
distance égale à 10m .La force ![]() fait un angle α avec la direction du déplacement. On donne f =15N.
Calculer les valeurs de W pour les angles : α =00 , α =300 α =1200 .Préciser
si le travail est moteur ou résistant.
fait un angle α avec la direction du déplacement. On donne f =15N.
Calculer les valeurs de W pour les angles : α =00 , α =300 α =1200 .Préciser
si le travail est moteur ou résistant.
Solution : α =0
cos α =1 W=150
J travail moteur
α =300 cos
α =0,866 W=129,9
J travail moteur
α =1200 cos α
=-0.5 W= —75 J travail résistant
TRAVAIL D’UNE
FORCE DE MOMENT CONSTANT APPLIQUEE A UN SOLIDE EN MOUVEMENT DE ROTATION AUTOUR
D’UN AXE
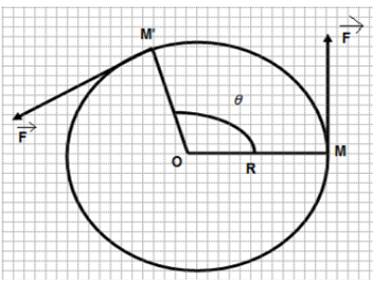
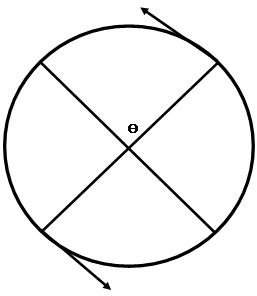
Considérons un solide (S) mobile autour d’un axe (Δ) passant par O,
perpendiculaire en O au plan de la figure. Lors de la rotation, le point
d’application de la force ![]() , constante, appliquée au solide, decrit un cercle de rayon MO situé dans
le plan de la figure.
, constante, appliquée au solide, decrit un cercle de rayon MO situé dans
le plan de la figure.
|
|
W MM’ =F. Soit M Δ ( WMM’=
M θ |
Conclusion : le travail d’une force de moment constant par rapport à l’axe de rotation
est égal au produit du moment de cette force par rapport à l’axe M Δ ( ![]() ) par l’angle balayé θ.
) par l’angle balayé θ.
TRAVAIL D’UN
COUPLE DE FORCE
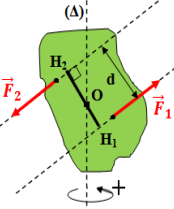
Soit θ, l’angle balayé
par chacune des forces du couple (C). Le travail du couple de forces (C), de
moment M, au cours d’une rotation d’angle θ, est égal à :
W=WF1 +WF2
=F1.H1O.θ +F2.OH2.θ=F.H1H2.
θ = F.d.θ //F1=F2 =F pour un
couple.
or F.d est le moment M du couple (C ) donc :
W(C)= M .θ
θ en radians
(rad)
M en Newton.metre (Nm)
W en joules (J)
Conclusion : Le travail d’un couple de moment constant M au cours d’une rotation
d’un angle θ est égal à W(C)
= M.θ
Remarques :
1-Ce résultat est
général chaque fois qu’une force ou un couple de moment constant est appliqué à
un solide en rotation.
2-L’angle de rotation
peut s’exprimer en fonction du nombre de tours n effectués par la relation θ=2πn
PUISSANCE
D’UNE FORCE
Un travail
peut être effectué dans un temps plus ou moins long d’où la nécessité
d’introduire une nouvelle notion : celle de la puissance qui fait
intervenir le travail et le temps mis pour l’effectuer.
Puissance
moyenne
La puissance moyenne d’une force est le quotient du
travail effectué par cette force par le temps mis pour l’effectuer :

W en J
t en s
P en W
Unité de la puissance : Dans le système international (SI), l’unité de
puissance est le watt (W).
Multiples : le
kilowatt : 1 KW=1000 W
Le mégawatt : 1 MW=1000KW=1000000W
Le gigawatt : 1 GW= 10000MW=1000000000W
On utilise aussi le cheval –vapeur(ch) : 1 ch=736 Watts
Puissance
instantanée
Cas d’un solide
en translation
Soit
F une force appliquée en un point A du solide (S). Si v est la vitesse du point
A à un instant donné, la puissance de F à cet instant est définie par :
![]()
NB : Si la force ![]() constante, est appliquée en un point du solide en mouvement
rectiligne uniforme, la puissance de la force est constante. Elle est donc
égale à la puissance moyenne.
constante, est appliquée en un point du solide en mouvement
rectiligne uniforme, la puissance de la force est constante. Elle est donc
égale à la puissance moyenne.
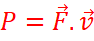
Cas d’un solide
en rotation autour d’un axe
Soit une force ![]() , de moment MΔ (
, de moment MΔ (![]() ), appliquée en un point A d’un solide mobile autour d’un axe
Δ. Si ω est la vitesse angulaire du solide à l’instant t, la
puissance de
), appliquée en un point A d’un solide mobile autour d’un axe
Δ. Si ω est la vitesse angulaire du solide à l’instant t, la
puissance de ![]() à cet instant est par définition :
à cet instant est par définition :
![]()
P = MΔ .ω
avec ω=2πN (rad/s)
N étant la vitesse de rotation en trs/s
Remarque :
1-Si le moment de la force ![]() est constant et si le mouvement du solide est un
mouvement de rotation uniforme, la puissance de la force est constante et égale
à la puissance moyenne :
est constant et si le mouvement du solide est un
mouvement de rotation uniforme, la puissance de la force est constante et égale
à la puissance moyenne :
EXERCICES
EXERCICE
I :
Une force d’intensité F=50 N se déplace sur une
distance d=30 m. Calculer le travail de cette force dans les cas
suivants :
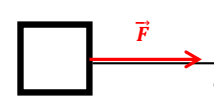
1.
La
force et le déplacement sont dans la même direction.
2.
La
force et le déplacement font entre elles un angle 30°.
3.
La
force et le déplacement sont perpendiculaires.
EXERCICE
II :
Ali tire sur son camion
par l’intermédiaire d’une ficelle avec une force ![]() d’intensité 3 N. La ficelle fait un angle de 20°
avec l’horizontale. Calculer, au cours d’un déplacement du camion de 4 m.
d’intensité 3 N. La ficelle fait un angle de 20°
avec l’horizontale. Calculer, au cours d’un déplacement du camion de 4 m.
1.
Le
travail de la force![]() .
.
2.
Le
travail du poids du camion.
EXERCICE
III :
Une roue verticale, mobile autour d’un axe
horizontal (Δ). Elle est soumise à trois forces ![]() ,
,![]()
![]() et
et ![]() situées dans son plan.
situées dans son plan.
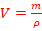
Sens de ![]() positif
positif
Sens de ![]() : contraire au sens
positif
: contraire au sens
positif
Point d’application de ![]() : Point O, centre de
rotation
: Point O, centre de
rotation
Calculer le travail de chacune de ces
forces en 2 tours de roue. On donne :
FA=2 N, FB=1N, FC=2,5N
Rayon de la roue : 20cm
Angle
![]() =90°
=90°
Angle
![]() =30°
=30°
EXERCICE
IV :
La puissance d’une turbine d’une usine hydroélectrique
est de 20MW. La hauteur de chute de chute d’eau qui alimente la centrale est de
750 m.
1. Quel serait le débit de chute s’il n’y avait
pas de perte d’énergie ?
2. Quel est en fait le débit si le rendement de
la turbine est 75% ?
EXERCICE
V :
Une voiture de masse 1t roule à la vitesse de
90 km/h sur une route rectiligne et horizontale. La puissance développée par le
moteur est. 7,5kW.
1. Quelle est l’intensité de la force
motrice ?
2. Quelle est la réaction de la route ? (On
suppose que les frottements sont négligeables)
3. Quel est le travail de toutes ces forcés
pour un déplacement rectiligne de 2km.
On donne :g=10N/kg
EXERCICE VI :
Une voiture de masse 1t monte à la vitesse de
90km/h une côte de 5%. Les résistances équivalent à une force parallèle au
déplacement et d’intensité 300N.
1. Faire le bilan de toutes les forces
appliquées à la voiture.
2. Calculer la puissance de la force motrice.
3. Quel est le travail de toutes les forces
pour un déplacement rectiligne de 2km. On donne : g=10N/kg
EXERCICE VII :
Un moteur tournant à 3600tr/mn, développe une
puissance de 9 kW.
1. Quel est le moment du couple moteur ?
2. Sachant quel le rotor est un cylindre de
diamètre d=20 cm. Calculer l’intensité
de la force motrice.
CORRIGES :
EXERCICE I :
1. Travail de la force![]() : Wforce=F.l=50x30=1500
J. // α=0 =>Wforce=
: Wforce=F.l=50x30=1500
J. // α=0 =>Wforce=![]() =F.lcosα=
50x30cos0=1500
=F.lcosα=
50x30cos0=1500
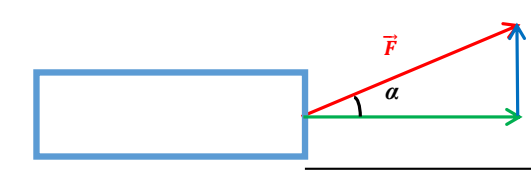
2. Travail de la force![]() :
:
.
. . .
Wforce=F.lcosα=50x30cos30=1300
J.
3.
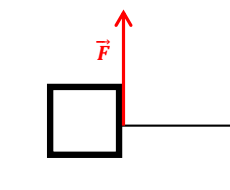
Wforce=F.lcosα=50x30cos90=0. . . // car
cos90=0
EXERCICE II :
1. Travail de la force![]() : Wforce=F.lcosα=3.4cos20=11,2J.
: Wforce=F.lcosα=3.4cos20=11,2J.
2. Travail du poids du
camion ![]() : Wpoids
=Plcocs90=0.
: Wpoids
=Plcocs90=0.
EXERCICE III :
Travail de ![]() A : WFA = MΔ(FA).θ=
FA x r x θ= FA x r x 2
A : WFA = MΔ(FA).θ=
FA x r x θ= FA x r x 2![]() n=2x0,2x2x3,14x2=5
J. // En n tours, l’angle balayé est : Ѳ = 2πn
n=2x0,2x2x3,14x2=5
J. // En n tours, l’angle balayé est : Ѳ = 2πn
Travail de ![]() B : WFB = MΔ(FB).θ=-
FB x rcos30 x θ=-1x0,2cos30x4x3,14= -1,256 J.
B : WFB = MΔ(FB).θ=-
FB x rcos30 x θ=-1x0,2cos30x4x3,14= -1,256 J.
Travail de ![]() C : WFC = MΔ(FC).θ=-
FB x0 x θ=0
C : WFC = MΔ(FC).θ=-
FB x0 x θ=0
EXERCICE IV :
1. Calcul du
volume :
P =W/t=mgh/t => m=Pt/gh or m=ρV
![]() = >
= >![]() =
=![]() =
=![]()
Calcul du
débit :
![]()
2. ![]()
EXERCICE V :
1. Conversion de la vitesse :
v=90x1000/3600=25m/s
Intensité de la force
motrice :P=Fv=>F=P/v=7,5.103/25=300N //P=![]() =
=![]() =Fv
=Fv
2. R=P=mg=1000x10=10000N.
3. Travail de la force
motrice :WF=Fxd=300x2000=600000J=600kJ
Travail du poids et de la
réaction : WP=WR=0 //P et R
sont perpendiculaires au déplacement.
EXERCICE VI :
Conversion de la vitesse :
v=90x1000/3600=25m/s
2.F=f+Px= f
+mgsinα
=300+1000x10sinα=300+10000x0,05=800N
Puissance de la force
motrice :P=Fv=800x25=20000 J .
3. Travail de la force
motrice :WF=Fxd=800x2000=1600000J=1600kJ
Travail du poids : WP=Pdsinα =10000x2000x0,05=1000kJ
Travail de la réaction : WR=0
Travail de la force de frottement :Wf=fxd=300x2000=600kj
EXERCICE VII :
1.P=MΔ. ω
=> MΔ =P/2πN
ω=2пN=2x3,14x3600/60= 376,8 rad/s
MΔ=P/2πN=9.103/376,8= 23,9 Nm.
2.F=MΔ/d=23,9/0,2=119,5 N.
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire