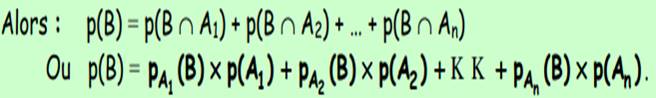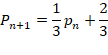PROBABILITÉS
GENERALITES
Définitions :
Expérience aléatoire :
Une expérience (lancé un dé par exemple) est aléatoire
lorsqu’elle a plusieurs résultats ou issues et que l’on ne peut pas prévoir, à
priori, quel résultat se produira.
Exemples :
- On lance une pièce de monnaie et on regarde
la face supérieure.
-
On lance un dé à six faces et on regarde le nombre de points inscrits sur la
face du dessus.
- On fait tourner une roue marquée sur ses
secteurs de couleurs différentes et on regarde le secteur marqué par la flèche.
Univers :
Soit E une expérience aléatoire donnant un nombre
fini de résultats possibles, l’ensemble des résultats possibles est appelé univers.
On le note :U ou Ω.
Eventualités :
Les éléments de l’univers Ω sont appelés éventualités.
Événement :
On appelle évènement les sous-ensembles
de l’univers Ω
-L’événement
formé d’un seul élément est appelé événement élémentaire.
-L’ensemble
vide est l’événement impossible.
-Lorsque
c’est tout l’ensemble Ω, l’événement est
certain.
Exemples :
Expérience
aléatoire : lancer d’un dé de 6 faces.
Eventualités :1
ou 4 par exemple //résultats possibles
Univers : Ω ={1,2,3,4,5,6}.
//ensemble des
résultats possibles de l’expérience.
Un
évènement A: ‘’obtenir le chiffre 4’’
Un
évènement B : ‘’obtenir le chiffre 6’’
Ω étant l’univers des éventualités d’une
expérience aléatoire, A et B des évènements de Ω
-l’évènement
(A ou B) est la partie AUB //obtenir 4 ou 6
-l’évènement
(A et B) est la partie A⋂B //obtenir 4 et 6
-
l’évènement contraire de A est la partie ![]()
-On
dit que l’évènement
A et l’évènement B sont incompatibles lorsque l’évènement (A et B) est
impossible
c.-à-d. A⋂B= ∅.
Probabilité d’un évènement
Définition
Soit Ω
l’univers des événements d’une expérience aléatoire, on dit que l’on a défini
une probabilité p sur Ω lorsque , a tout événement A
de Ω, on
peut associer un nombre réel appelé
probabilité de A noté p(A) vérifiant les conditions suivantes :
-0≤p(A)≤1
- p(Ω )=1 et p(∅. )=0;
-La probabilité d’un événement est égale à la
somme des probabilités des événements élémentaires qui le constituent.
Ainsi, si A={ x1 ,x2,…,
xn }

Propriétés
Soit p une probabilité sur l’univers Ω , A et B deux événements de Ω. Alors :
-P(AUB)=P(A)+p(B) -
P(A⋂ B),
-Si A et B sont incompatibles si et seulement si
A⋂ B=ø alors P(A⋂ B)=0 et P(AUB) = P(A)+P(B).
-A
et son événement contraire ![]() forment une partition de Ω donc p(Ω)=p(A) + p(
forment une partition de Ω donc p(Ω)=p(A) + p(![]() ) soit P(
) soit P(![]() ) =1- P(A).
) =1- P(A).
Résumons :

Exemple
: On considère
l’expérience aléatoire suivante : On tire une carte dans un jeu de 32 cartes à
jouer. On considère les événements suivants :
A
: « On tire un valet » P(A)=1/8
B
: « On tire un roi » P(B) = 1/ 8
Les deux évènements A et B sont incompatibles,
en effet A ∩ B = ∅.
On en déduit que la probabilité de l’évènement
« Tirer un valet ou un roi » est égale à :
P(A∪B) = P(A)+P(B) =1/8 + 1
/8 = 1/4
Calculs des probabilités
Soit p une probabilité définie sur l’univers Ω des éventualités d’une
expérience aléatoire, on dit qu’il y a équiprobabilité, si tous les
évènements élémentaires de U ont la même
probabilité.
Dans
ce cas, pour tout évènement A de Ω


VARIABLES ALEATOIRES
Définition
Soit un univers
fini Ω,
Une variable
aléatoire X est une application définie de Ω dans IR.
L’ensemble X(Ω) des éléments que peut
prendre X s’appelle univers image.
Si X(Ω) = (x1, x2,…,xn), on note
(X=xi), l’ensemble des éléments de Ω
ayant pour image xi par X ; c’est aussi l’évènement ‘’X prend la valeur xi’’.
Loi
de probabilité
Soit X une variable aléatoire définie sur l’univers Ω
munie d’une probabilité p, la loi de probabilité associée à X est
l’application définie de [0,1] dans IR, qui a xi ϵ X(Ω) associe
p(X=xi).
Remarque :
Pour définir une loi de probabilité associée à X, il suffit de se
donner les probabilités élémentaires p(X=x1), p(X=x2),…,
p(X=xn) telle que 
Fonction de répartition
La[H1] fonction de répartition de la variable
aléatoire X est la fonction
F :IR→IR
X→p(X<x)
Paramètres d’une variable
aléatoire
·
On appelle espérance
mathématique d’une variable aléatoire X, le réel E(X) défini par :
·
On appelle variance d’une variable
aléatoire Xi, le réel V(X) défini par :
·
L’écart-type
 d’une variable aléatoire X est la racine
carrée de la variance
d’une variable aléatoire X est la racine
carrée de la variance
PROBABILITES
CONDITIONNELLES
Définition
p
désigne une probabilité sur un univers fini Ω. A et B étant deux
évènements de Ω, B étant de probabilité non nulle. On appelle probabilité
conditionnelle de l’évènement A sachant que B est réalisé le réel
noté :
Le réel p(A/B) se note aussi pB(A)
et se lit aussi’’ probabilité de A sachant B’’.
Remarque : Si A et B sont tous deux de
probabilité non nulle, alors les probabilités conditionnelles p(A/B) et p(B/A)
sont toutes les deux définies et on a :
p(A ∩ B) = p(A/B) ×p(B)
= p(B/A) × p(A).
Evènements
indépendants
Deux
événements A et B de probabilité non nulle sont indépendants si et seulement
p( A ∩ B) = p(A)p(B).
Remarque :
Si p(A)≠0 et p(B)≠0,
alors A et B sont indépendants lorsque pB(A)=p(A)
ou bien pA(B)=p(B)
Formules
des probabilités totales
Soient A1, A2, …, An une
partition de l’univers Ω constituée d’événements de probabilités non
nulles et B un événement quelconque contenu dans Ω.
EXERCICE
I :
On dispose d’un jeu de 32 cartes, on prend simultanément 8,
ce qui constitue une main. Quelle est la probabilité
1. D’avoir exactement 2 as ?
2. D’avoir aucun as ?
3. D’avoir au moins un as ?
4. D’avoir exactement 2 cœurs et 3 piques ?
EXERCICE
II :
1.On considère
l’expérience aléatoire suivante : On lance un dé à six faces et on regarde le
nombre de points inscrits sur la face du dessus. On considère les événements
suivants :
A : « On obtient
un nombre impair »
B : « On obtient
un multiple de 3 »
Calculer la
probabilité de l’évènement A∪B.
EXERCICE III :
Un jeu consiste à lancer deux fois de suite une pièce de monnaie.
Lorsqu’on a pile, on gagne 2 points. Lorsqu’on a face, on perd 1 point. On
définit une variable aléatoire ‘’somme des gains’’.
1.
Donner la loi de probabilité de X
2.
Calculer l’expérience mathématique, la variance et l’écart-type de X.
EXERCICE
IV :
On lance trois fois de suite une pièce de monnaie
équilibrée. On gagne 2 € pour chaque résultat « pile » et on perd 1 € pour
chaque résultat « face ».
1°) Quel est l’ensemble E des issues possibles ?
2°) Soit X l’application de E dans R qui, à chaque issue, associe le gain correspondant.
a) Quelles sont les valeurs prises par X ?
b) Quelle est la probabilité de l’événement « obtenir un gain de 3 € »
? On note cette probabilité p(X = 3).
EXERCICE V :
On lance deux fois un dé pipé
tel que P(1)=P(3)=P(4)=1/2 et P(2)=P(6)=1/4.
Quelle est la probabilité que la somme des
points obtenus soit supérieure à 10 (strictement) sachant que :
1. Un des
résultats est 6.
2. Le premier
résultat est 6.
EXERCICE
VI :
On considère une succession de sacs qu’on désigne par S1,
S2, …, Sn …
Au départ le sac S1 contient 2 jetons noirs et 1 jeton blanc ; tous les
autres sacs contiennent chacun 1 jeton noir et 1 jeton blanc. On tire au hasard
un jeton du sac S1 que l’on place dans le sac S2. Puis,
on tire au hasard un jeton du sac S2, que l’on place dans le sac S3,
et ainsi de suite.
On note Bk l’évènement : « le jeton tiré du sac Sk
est blanc », et pk=P(Bk) sa probabilité.
Dire si les propositions suivantes sont vraies ou fausses
a.
On
a :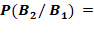
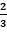
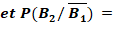
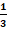
b.
Pour tout entier n≥1 :
Pour tout n ϵ N*, on
pose 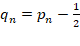
c.
Alors la suite qn est arithmétique
d.
La suite pn converge vers 2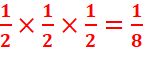
CORRIGES
EXERCICE
I :
1. 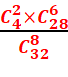
2. 
3. 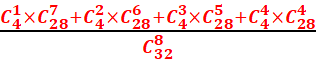
4. 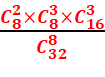
EXERCICE
II :
P(A)=
1 /2 et P(B)= 2/ 6 = 1/ 3
A∩
B est l'événement élémentaire : « On obtient un 3 », donc : P( A∩ B) = 1/
6
L'événement
A∪ B a
donc pour probabilité : P(A ∪ B) =
P(A) + P(B) − P(A ∩ B) = 1 /2 + 1 /3 – 1/ 6 = 3 /6 + 2 /6 − 1
/6 = 4/ 6 = 2/ 3
EXERCICE III :
1.Le tableau ci-dessous donne
l’ensemble des éventualités forme des couples (F,P)
|
|
F
|
P
|
F
|
(F.F)
|
(F,P)
|
P
|
(P,F)
|
(P,P)
|
CardΩ=4, l’univers image
X(Ω) est donne par :
X(Ω)= {-2,1,4)
L’hypothèse d’équiprobabilité est
vérifiée car le lancer se fait par hasard
P(X=xi) =card(X=xi)/ CardΩ
Le tableau suivant donne la loi de
probabilité
xi
|
-2
|
1
|
4
|
P(X=xi)
|
1/4
|
2/4
|
1/4
|
2.E(X)=-2.1/4
+1.2/4+4.1/4=-1/2+1/2+1=1
EXERCICE
IV :
1.(PPP)→6
(FFF)→-3
(PPF)→3
(PFF)→0
2.
a)X(E)={-3,0,3,6}
loi de
probabilite X
b)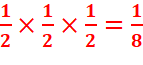
EXERCICE V :
EXERCICE VI :
Avez-vous un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire