PENDULE CONIQUE
Un système formé d’un
solide (S) de petites dimensions (de masse m et de centre d’inertie G) suspendu
à un fil de longueur l et décrivant une trajectoire circulaire horizontale
constitue un pendule conique. Le système est nommé ainsi car dans son
déplacement, la corde décrit la forme d’un cône. Dans le référentiel de
laboratoire, considéré comme galiléen, le solide (S) est soumis à deux
forces : son poids 
et la tension
du fil.
D’après le TCI :
Lorsque le pendule est
incliné d’un angle θ par rapport à l’horizontal, la projection de cette
relation donne (dans un repère (G, I, J) choisi tel que (G, I) soit dans la
direction du rayon r de la trajectoire, orienté vers le centre, et (G, J) soit
vertical.
Par projection sur les
deux axes, on a :
Tsinθ=man=mv2/r (1)
Tcosθ=mg (2)
La force centripète
correspond à la composante horizontale Tsinθ de
la tension.
La valeur de
l’accélération centripète du centre d’inertie de G est an=r
=lsinθ car
r=lsinθ.
En divisant (1) par
(2), on obtient :
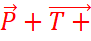
Soit à condition que sinθ
,
.
Cette solution n’est possible
que si :
car 
La valeur minimale de la vitesse angulaire est
donc
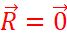
Elle dépend de la
longueur du pendule.
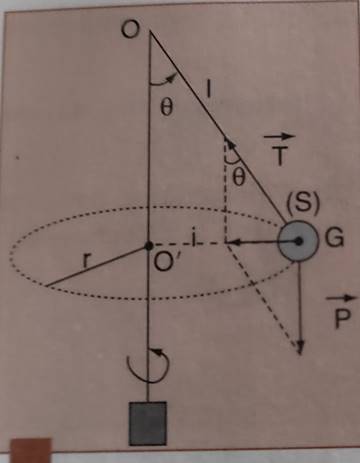
Cette condition étant
remplie, en remplaçant cosθ par sa valeur, on
trouve :
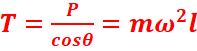
EXERCICES
EXERCICE I :
On fait tourner une pierre de 2 kg attachée à une
corde avec une vitesse de 3,6 km/h. La longueur de la corde est de 1 m.
a) Quelle est l’accélération de la pierre ?
b) Quelle est la tension de la corde ?
EXERCICE II :
Un point matériel M de masse m
est suspendu à un fil de longueur L inextensible et de masse négligeable
attaché en un point fixe O' de l'axe Oz. M décrit un cercle de rayon R de
centre O à la vitesse angulaire ω constante dans le plan Oxy
a) Calculer la tension du fil.
b) Calculer l'inclinaison α du fil par
rapport à la verticale.
c) A quelle condition sur ω ce mouvement
peut-il avoir lieu ?
EXERCICE III :
Un pendule conique est constitué d’une boule
métallique quasi ponctuelle de masse m=60g suspendue à un fil inextensible de
longueur l=80 cm et de masse négligeable, tournant à la vitesse angulaire
ω autour d’un axe vertical.
Pour une valeur suffisante de ω le fil
s’incline d’un angle ϴ et la boule décrit dans un plan horizontal un
mouvement circulaire uniforme de centre O.
1. Appliquer le théorème du centre d’inertie dans un
référentiel approprié et établir la relation entre la vitesse angulaire ω
et l’angle ϴ.
2. Quelle est la valeur minimale ω0
de ω en dessous de laquelle ϴ=0 ?
3. Calculer la tension du fil pour ϴ=30°, puis
pour ω=10rad.s-1, puis pour ω=4rad.s-1.
EXERCICE IV :
On
dispose d’un ressort à spires non jointives de longueur au repos l0
et de raideur K. On néglige la masse du ressort dans tout l’exercice. On enfile
ce ressort sur une tige OT, soudée à un axe verticale ∆ faisant avec la
verticale descendante un angle Ѳ (Ѳ <90°). Une des extrémités du
ressort est fixée en O, tandis qu’à l’autre on accroche un corps de masse m,
coulissant sans frottements sur OT (fig 3). Le système est
au repos.
1.
Faire l’inventaire des forces appliquées au
corps C.
2.
Calculer la longueur du ressort l1 à
l’équilibre.
Calculer
l’intensité de la force R exercée par la tige OT sur le corps C.
On
donne : l0 = 0,2m ; k=25 N/m ; Ѳ=30° ;
m=200 g ; g=9,8 N/kg.
3.
La tige étant supprimée, l’ensemble tourne
autour de
l’axe (∆)
à la vitesse angulaire constante ω ; le ressort n’oscille
pas et a une longueur l2.
3.1 Préciser la trajectoire
décrite par le corps C.
3.2 Exprimer la longueur l2
en fonction de ω, m, Ѳ, K, et l0.
3.3 Calculer l2
sachant que ω=7rad/s.
EXERCICE V :
Un axe vertical (Δ) sur lequel est fixé
une tige (t) tourne à la vitesse constante ω. On enfile sur la tige un
ressort(R) de masse négligeable et de raideur k, fixé en O et portant à son
extrémité libre un anneau (Δ), de masse m. Le ressort et l'anneau
coulissent sans frottements sur la tige (t).
1. Détermine l’allongement du ressort en
fonction de ω, m, k, et l longueur du ressort à
vide.
2. AN :
m=50g, ω=2пrad.s-1, k=0,1N.cm-1,l=15cm.
3. La limite d’élasticité du ressort est
atteinte lorsque l’allongement du ressort est égal à 25 cm. Calculer (en tr/s)
la fréquence maximale permise.
EXERCICE VI :
Un
axe vertical (Δ) sur lequel est fixé une tige (t) tourne à la vitesse
constante ω. On enfile sur la tige un ressort(R) de masse négligeable et
de raideur k, fixé en O et portant à son extrémité libre un anneau (Δ), de
masse m. Le ressort et l'anneau coulissent sans frottements sur la tige (t).
1.
Détermine l’allongement du ressort en fonction de ω, m, k, et l longueur du ressort à vide.
2. AN : m=50g, ω=2пrad.s-1, k=0,1N.cm-1,l=15cm.
3.
La limite d’élasticité du ressort est atteinte lorsque l’allongement du ressort
est égal à 25 cm. Calculer (en tr/s) la fréquence maximale permise
CORRIGES :
EXERCICE
I :
a)
v=3,6
x1000/3600=1m/s
a=v2/l=12/1=1
m.
b)
v=lω =>ω=v/l=1/1=1rad/s
T=mω2l=2x12x1=2N
EXERCICE
II :
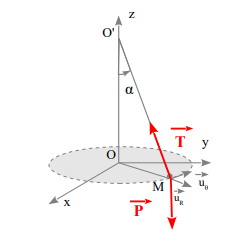
a)
Bilan des forces :
• Poids : ⃗P
•
Tension du fil : ⃗T
D’après le TCI : m⃗a=⃗P+⃗T
• Par projection suivant ⃗uR :
−m Rω2=−T
sinα or R=L sinα d'où T=mLω2 .
b) Calculer l'inclinaison α du fil par
rapport à la verticale.
• Par projection suivant ⃗uz :
0=−m
g +T cosα =>cosα= mg/T d'où cosα= g/ Lω2
c)
Ce mouvement est possible si les
paramètres du problème vérifient : cosα≤1 d'où ω≥√
g/ L .
EXERCICE
III :
1.
Par projection sur les deux axes, on a :
Tsinθ=man
(1)
Tcosθ=mg (2)
2.
Soit à condition que sinθ ≠0 , g/ω2 = cosθ.
Cette solution n’est possible que si g/ω2 ≤1(car
cosθ≤1) ou ω2≥g/l. La valeur minimale de la vitesse angulaire
est donc :
.
Elle dépend de la longueur du pendule.
.
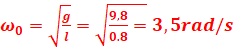4.
ϴ=30° :
ω=10rad.s-1 : T=0,06x100x0,8=4,8N.
ω=4rad.s-1 : 
=0,06x16x0,8=0,768N.
EXERCICE IV :
1.
Poids du corps C
Tension du ressort
Réaction de la tige
2. 
Par
projection :
T-mgcosθ=0
or T=kΔl=k(l1-l0)
< => k(l1-l0)=
mgcosθ
=>l1=l0+
mgcosθ/k
l1=l0+
mgcosθ/k
=0,2+0,2x9,8xcos30/25=0,28m
3.
Par projection :
R-mgcosθ=0=>R=
mgcosθ=0,2x9,8cos30=0,98N.
4.
4.1.Le corps C décrit une trajectoire circulaire de centre O’
situe sur l’axe Δ et de rayon r=l2sinθ
4.2 Le TCI
applique au solide C s’exprime par la relation : P+T=ma
L’accélération
du centre d’inertie du solide C est dirigée vers le
centre O’ de la trajectoire et a pour valeur :
aG=rω2=l2ω2sinθ
La
construction graphique permet d’écrire :
tanα=maG/mg=l2ω2sinθ/g
soit :
sinθ/cosθ= l2ω2sinθ/g=>cosθ=g/ω2l2 avec cosθ=P/T= ω2l2=>T=mω2l2
d’autre part : T=k(l2-l0).
Les deux
relations impliquent : k(l2-l0) = mω2l2=>l2=kl0/(k-mω2)
4.3. l2=25x0,2(25-(0,2x72))=0,33m