SUITES ARITHMETIQUES ET GEOMETRIQUES

SUITES ARITHMETIQUES

La suite (u_n) est une suite arithmétique s’il existe un nombre réel r tel que pour tout naturel n,

u_n+1= u_n+ r

Le réel r est appelé la raison de la suite.

Propriétés :

Pour tout entier naturel n,

u_n = u₀ + nr .

Pour tous entiers naturels n et p ,

u_n = u_p + ( n – p ) r

Somme de n termes consécutifs d’une suite arithmétique

Exemple :

On pose : Sn=1+2+3+…+n

Calculons la somme Sn

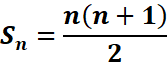
· Si on a n+1 termes :

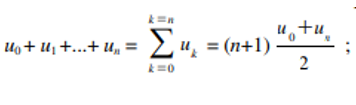
Si le premier terme est u₀et la raison est r

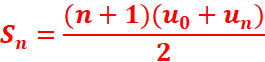
D’une façon générale, la somme Sn des premiers termes d’une suite arithmétique vérifie :

Sn= u_p+ u_p+1+ · · · + u_n

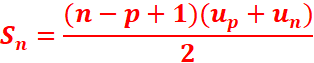
SUITES GEOMETRIQUES

La suite (u_n) est une suite géométrique s’il existe un nombre réel q tel que pour tout naturel n ,

u_n+1 = qu_n .

Le réel q est appelé la raison de la suite.

Propriétés :

Soit une suite géométrique de premier terme u₀ et de raison q. alors pour tout entier naturel n , on a :

u_n = u₀ × q ⁿ .

Pour tous entiers naturels n et p ,

u_n = u_p× q ^{(n
– p)} .

Somme de n termes consécutifs d’une suite géométrique

Soit un une suite géométrique de premier terme u₀ et de raison q

S_n=u₀+ u₁ + · · · + u_n

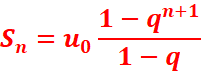
Soit un une suite géométrique de premier terme u_p et de raison q

S_n= u_p+u_p+1+…..+u_n

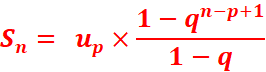
p étant le nombre de terme de la somme (n-p+1)

➪ D’une façon générale, la somme Sn des premiers termes d’une suite géométrique vérifie :

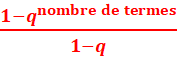
Limites

Soit q un reel positif

EXERCICES

EXERCICE I :

U_n est une suite arithmétique de raison r et de premier terme u₀. Sachant que u₃=5 et S₄=15,

1.Calculer r et u₀

2.Deduire le terme général de u_n

3.Calculer

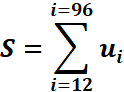
EXERCICE II :

On considère les suites u_n et v_n définies par :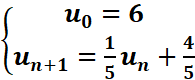

1.Demontrer que v_n est une suite géométrique dont on déterminera le premier terme et la raison.

2.Exprimez v_n en fonction de n

3.Calculer la limite de s_n quand n→∞

EXERCICE III :

On considère les suites u_n et v_n définies par :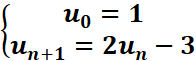

1.Calculer u₁, u₂ et u₃

2.Demontrer que v_n est une suite géométrique dont on déterminera le premier terme et la raison

3.Donner l’expression du terme général de v_n

4. On pose :s_n=v₀+v₁+v₂+v₃+…….+v_n

Donner l’expression de S_n en fonction de n

5.Calculer la limite de s_n quand n→∞

EXERCICE IV :

Dans un pays, au début de l’année 2008, une ville A compte 200 000 habitants, et sa population décroît de 3% par an, tandis qu’une autre ville B compte 150 000 habitants, avec une croissance annuelle de 5%. On appelle an le nombre d’habitants de A _n années après 2008 (d’où u₀=200 000), et de même b_n pour la ville B.

1) Calculer a₁ et b₁

2) Montrer que a_n et bn sont des suites géométriques dont on précisera les caractéristiques. Puis donner leur forme explicite.

3) Au bout de combien d’années la population de la ville B dépassera-t-elle celle de la ville A ? La population de B augmente, celle de A diminue. Quand aura-t-on a_n=b_n ?

4.Une population d’insectes augmente de 30% par an. Aujourd’hui, elle compte un million d’individus. On veut savoir au bout de combien d’années elle atteindra 100 millions.

EXERCICE V :

Soit 𝑎 ∈ ] 1/ 2 ; 1[ et les suites (𝑢_𝑛 ) 𝑒𝑡 (𝑣_𝑛 ) telles que 𝑢₀ = 2 ; 𝑣₀ = 3 ,𝑢_𝑛₊₁ = 𝑎𝑢_𝑛 + (1 − 𝑎)𝑣_𝑛 𝑒𝑡 𝑣_𝑛₊₁ = (1 − 𝑎)𝑢_𝑛 + 𝑎𝑣_𝑛.

1) Démontre par récurrence que pour tout entier 𝑛 ∈ ℕ, 𝑣_𝑛 − 𝑢_𝑛 > 0.

2) a- Démontre que la suite (𝑢_𝑛 ) est croissante.

b- Démontre que la suite (𝑣_𝑛 ) est décroissante.

c- Démontre que les suites (𝑢_𝑛 ) 𝑒𝑡 (𝑣_𝑛) sont convergentes.

3) Soit la suite (𝑤_𝑛 ) définie par 𝑤_𝑛 = 𝑣_𝑛 − 𝑢_𝑛 .

a- Démontre que la suite (𝑤_𝑛) est une suite géométrique à déterminer.

b- En déduire que les suites (𝑢_𝑛 ) 𝑒𝑡 (𝑣_𝑛) ont la même limite.

4) Soit la suite (𝑡_𝑛 ) définie par 𝑡_𝑛 = 𝑢_𝑛 + 𝑣_𝑛 .

a- Démontre que la suite (𝑡_𝑛 ) est une suite constante.

b- En déduire la limite commune des suites (𝑢_𝑛 ) 𝑒𝑡 (𝑣_𝑛).

CORRIGES

EXERCICE I :

U₃=u₀+3r

S₄=(n+1)(u₀+u₄)/2=5(2u₀ +4r)/2

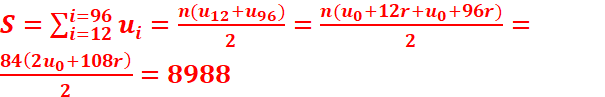
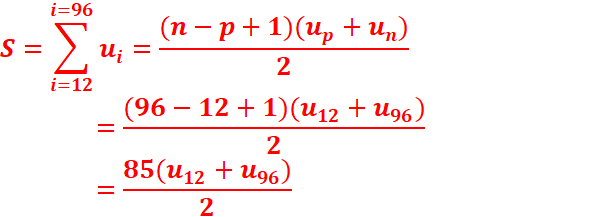
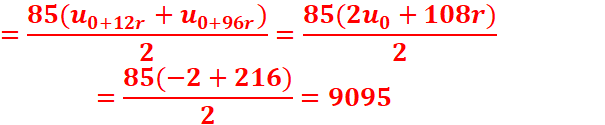
EXERCICE II :

1.v_n+1=u_n+1-1=1/5u_n +4/5 -1=1/5v_n=>suite géométrique de raison q=1/5

v₀=u₀-1=6-1=5

2.v_n=v₀qⁿ=5(1/5)ⁿ

3.v_n=u_n-1=>u_n=5(1/5)ⁿ+1

EXERCICE III :

1. u₁=u₀₊₁=2u₀-3=2x1-3=-1

u₂=-5

u₃=-13

2.v_n+1=u_n+1-3=2u_n -3 -3=2u_n-6=2(u_n-3)=2v_n

v₀=u₀-3=1-3=-2

q=2

3.v_n=v₀qⁿ=(-2)(2)ⁿ=-2ⁿ⁺¹

4.S_n=v₀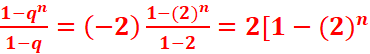

EXERCICE IV :

a₁=200 000 – (3/100) 200 000= 194 000

b₁=150 000 + (5/100) 150 000= 157 500.

a_n+1= a_n – (3/100) a_n = (97/100) a_n = 0,97 an, et de même b_n+1= 1,05 b_n .

On en déduit que a_n = a₀ (0,97)ⁿet b_n = b₀ (1,05)ⁿ .

Cela aura lieu lorsque 0,97ⁿ 200 000 = 1,05ⁿ 150 000, soit (1,05/0,97)ⁿ = 20 / 15, ou (105 / 97)ⁿ = 4/3.

Passons en logarithmes : n (ln 105 – ln 97) = ln 4 – ln 3, d’où ln 4 ln 3 ln105 ln 97 => n = 3,63. La population de B dépassera celle de A au cours de la troisième année, c’est-à-dire pendant l’année 2008+3 = 2011.

4. Appelons u₀ la population actuelle, et un sa valeur au bout de n années. En un an, elle augmente de 30% = 30/100= 0,3. Cela signifie que u_n+1= u_n + 0,3 u_n = 1,3 u_n. On obtient une suite géométrique de terme initial u₀ et de raison 1,3. D’où la forme explicite u_n=1,3ⁿ 10⁶ . On veut trouver n tel que u_n=100. 10⁶ , c’est-à-dire 1,3ⁿ =100, ou encore n ln1,3 = ln 100, n = ln100 / ln1,3, n = 17,6 années.

EXERCICE V :

Avez-vous un exercice a proposer?Cliquez-ici

Merci de votre visite
Laissez un commentaire