Définition :
Une suite numérique (un) est une
application de IN dans IR.
(un) : IN→IR
n→un
On note (un)
la suite de nombres u0, u1, u2,...,
un, ...
Le nombre un
est le terme d’indice n (ou de rang n).
uo est le premier terme de la suite.
Suites
définies par une formule explicite
Ce sont des suites dont
l’expression directe est en fonction de l’entier n
Exemple : Un=2n +1
Calculons les 5
premiers termes
U0=2x0 +1=1
U1=2x1 +1=3
U2=2x2 +1=5
U3=2x3 +1=7
U0=2x4 +1=1
Suites
définies par une formule implicite ou par récurrence
Ce sont des suites
définies par la valeur du premier terme et une relation un+1=f(un)
pour tout n. Elles sont définies par une formule de récurrence (formule
de récurrence : un terme de la suite s’écrit en fonction du ou des précédents).
Exemple : un+1 = 3un + 2 et uo=1
Calculons les deux
premiers termes :
u1 =
3u0 + 2= 3x1 + 2=5
u2 =
3u1 + 2= 3x5 + 2=17
OPERATIONS
SUR LES SUITES NUMERIQUES
Soient ( Un )nϵ
I et ( Vn
)n ϵ I deux suites
numériques toutes définies sur une partie I de IN ;
Soit a un nombre réel. Alors
:
i)
La
suite somme (U+V )nϵ I est définie comme suit :
" Înϵ I on a (U +V)n=Un+Vn ;
ii)
La
suite produit (UxV)n est définie comme suit :
" Înϵ I on a (UxV)n=UnxVn
;
iii)
La
suite produit par un réel ( αU)nϵ I est définie comme suit :
" În I on a (aU)n=α Un .
Variations
d’une suite
Définition :
Soit
(un) une suite de nombre réels. E est son ensemble de définition et
I, un intervalle de E.
La suite (un)
est croissante si, pour tout entier naturel n, un+1 ≥un .
La suite (un) est
strictement croissante si, pour tout entier naturel n, un+1 > un .
La suite (un) est
décroissante si, pour tout entier naturel n, un+1 ≤ un
.
La suite (un) est
strictement décroissante si, pour tout entier naturel n, un+1 < un .
Méthode :
a) La méthode
algébrique
Ø On étudie le signe de un+1-un
·
Si
pour tout n de E, un+1-un≥0, alors la suite un
est croissante.
·
Si
pour tout n de E, un+1-un≤0, alors la suite un est
décroissante.
Exemple :
Ø Un compare le quotient
![]() à 1 ,
si pour tout entier naturel n de E, un≥1
à 1 ,
si pour tout entier naturel n de E, un≥1
·
Si
pour tout n de E, ![]() alors la suite un
est croissante.
alors la suite un
est croissante.
·
Si
pour tout n de E, ![]() alors la suite un
est décroissante.
alors la suite un
est décroissante.
Exemple :
b) Méthode à l‘aide
d’une fonction
Si un =f(n), alors un a le même sens de
variation que la fonction f.
On étudie donc les
variations de la fonction sur I contenant E.
·
Si
f est croissante sur I, alors la suite un est croissante.
·
Si
f est décroissante sur I, alors la suite un est décroissante.
Exemple :
Convergence
d’une suite
Définition :
Une suite (un)
est une suite convergente vers le nombre réel l
si tout intervalle ouvert contenant l contient tous
les termes de la suite à partir d'un certain rang. Le nombre réel l est la limite de la suite (un), on
écrit :
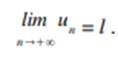
Une suite est divergente
si elle n’est pas convergente (sa limite est infinie ou n’existe pas).
.
REPRESENTATION
GRAPHIQUE DES TERMES D’UNE SUITE
Si la suite (un)
a son terme général défini en fonction de n, on
représente la suite dans un repère du plan, par un ensemble de points de
coordonnées (n; un). Cette représentation
graphique permet de visualiser les variations de la suite et éventuellement la
convergence.
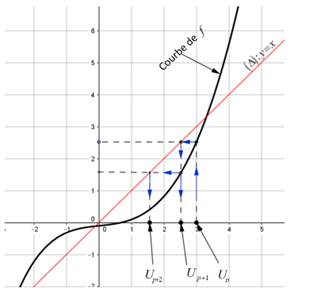
Méthode :
·
Commencer
par représenter la fonction et la première bissectrice y=x.
·
Placer
le point d’abscisse u0 sur l’axe des abscisses
·
A
partir du point d’abscisse u0 sur l’axe des abscisses, on obtient
sur l’axe le point d’abscisse u1 en traçant une parallèle à l’axe
des ordonnées qui coupe la courbe au point A0(u0, u1),
on trace ensuite une parallèle à l’axe des abscisses qui passe par A0 ;
cette parallèle coupe la première bissectrice en un autre point. En traçant une
autre parallèle à l’axe des ordonnées passant par ce point, cette nouvelle
parallèle coupe l’axe des abscisses au point u1.
·
On
répète le processus.
SUITES
ARITHMETIQUES
La suite (un)
est une suite arithmétique s’il existe un nombre réel r tel que pour tout
naturel n,
un+1 = un +
r.
Le réel r est appelé la
raison de la suite.
Propriétés :
Pour tout entier naturel n,
un = u0 + nr .
Pour tous entiers naturels n et p,
un = up + ( n – p ) r
Somme de n
termes consécutifs d’une suite arithmétique
Soit un une
suite arithmétique, la somme des termes de cette suite Sn=u1+u2+….+un est :
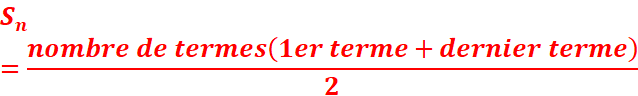
On pose :
Sn=1+2+3+…+n
Calculons la somme Sn
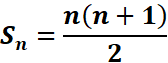
·
Si
on a n+1 termes :
Sn=u0+u1+u2+u3+…+un
![]()
D’une façon générale,
la somme Sn des premiers termes d’une suite arithmétique vérifie :
Sn=up
+ up+1 + · · · + un

SUITES
GEOMETRIQUES
La suite (un) est une suite géométrique
s’il existe un nombre réel q tel que pour tout naturel n ,
un+1 = qun .
Le réel q est appelé la
raison de la suite.
Propriétés :
Soit
une suite géométrique de premier terme u0 et de raison q. alors pour
tout entier naturel n , on a :
un = u0 × q n .
Pour tous entiers
naturels n et p ,
un = up× q (n – p) .
Somme de n
termes consécutifs d’une suite géométrique
Soit un une suite
géométrique de premier terme u0 et de raison q
Sn=u0 +
u1 + · · · + un
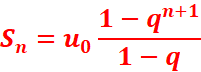
Soit un une suite
géométrique de premier terme up et de raison q
Sn=
up+up+1+…..+un
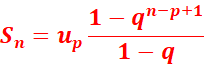
p étant le nombre de terme de la somme (n-p+1)
➪ D’une façon générale, la somme Sn des premiers termes d’une
suite géométrique vérifie :

Limites
Soit q
un reel positif
· ![]()
· ![]()
· ![]()
EXERCICES
EXERCICE
I:
1.un
est une suite arithmétique de premier terme u0 et de raison r.
Calculer
u0 et r sachant que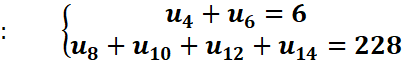
2. un est une
suite arithmétique de premier terme u0=2 et de raison r=3
On
pose :
![]()
a.
Exprimez S en fonction de n
b.
Déterminer n sachant que S=187
EXERCICE
II:
Soit
vn la suite définie par 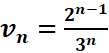
1.Determiner :
v0 et v1
2.Exprimez
vn+1 en fonction de vn.
3.En
déduire la nature de la suite vn. On
précisera sa raison.
4.Calculer
la limite de la suite vn.
5.quel
est le signe de vn+1-vn ? en déduire le sens de
variation de la suite vn.
6.On pose S=v0+v1+v2+….+vn
Exprimez
S en fonction de n.
EXERCICE
III:
On considère la suite (Un) définie par :
u0=30000
Un=u0 +
600000n
a) Donner
la nature de cette suite ainsi que ses éléments caractéristiques
b) Calculer
Sn = u0 + u1 +u2 +…….un en fonction de n.
EXERCICE IV :
Soit une suite (un) définie par :
u0 = 2
un+1 = 2un
+ 5
On pose la suite (vn)
telle que vn = un + 5
1) Montrer
que la suite (vn) est géométrique
2) Exprimer
vn puis un en fonction de n.
EXERCICE V :
On considère les suites un et vn définies par :
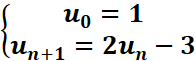
et
vn=un-3
1.Calculer u1,u2
et u3
2.Demontrer que vn
est une suite géométrique dont on définira le premier terme et la raison.
3.Donner l’expression générale de vn en fonction de n.
4.On pose Sn=v0 +v1+……vn
Donner l’expression de Sn en
fonction de n
5.Calculer la limite de Sn
quand n tend vers l’infini.
EXERCICE VI :
En Janvier 2005, une entreprise offrait sur le
marché 10000 articles d’un nouveau produit avec une perspective d’augmentation
de 5% par an. On note P0=10000 la production en l’an 2005 et Pn la quantité offerte en l’an 2005 + n, n étant
un entier naturel.
1-Calculer
P1, P2 et P3
2-Exprimer
Pn+1 en fonction de Pn,
pour tout entier naturel non nul.
En
déduire la nature de la suite (Pn), puis
exprimer (Pn) en fonction de n.
3-Calculer
la production prévisible de Janvier 2005 à Janvier 2009.
CORRIGES :
EXERCICE I:
1.un=u0 +nr
u4=u0
+4r
u6=u0
+6r=> u4 + u6= u0 +4r+ u0 +6r=2u0+10r
=> u0 +4r=3
u8=u0
+8r
u10=u0
+10r
u12=u0
+12r
u14=u0
+14r =>u8+u10+u12+u14= u0
+8r+ u0 +10r+ u0 +12r+ u0 +14r=4u0+44r
=>u0+11r=57
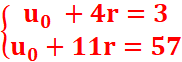
La résolution donne u0=-42 et r=9
2.
a-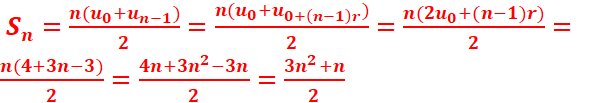
b-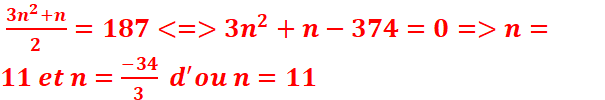
EXERCICE II:
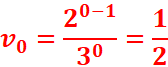
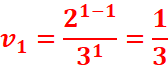
2. 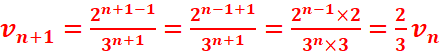
3. 
4. ![]()
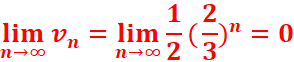
5.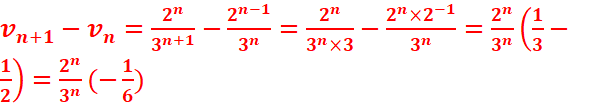
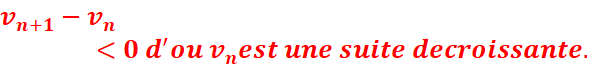
6. S=v0+v1+v2+….+vn
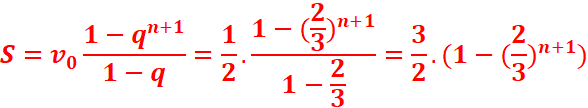
EXERCICE III:
a)
C’est une suite arithmétique de raison 60000 et de premier terme
30000.
b) 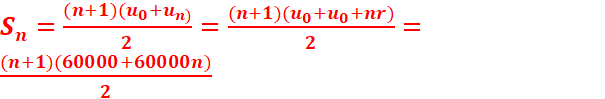
EXERCICE IV :
1.vn+1= un+1
+ 5=2un + 5+5=2un + 10=2(un + 5)=2vn
2.vn+1=2vn=>
vn est une suite géométrique de raison 2
et de premier terme v0=u0+5=2+5=7
vn=v0qn=7.2n
EXERCICE V :
1.u1=-1,
u2=-5
u3=-13
2.vn+1=un+1
-3=2un -3-3=2un-6=2(un-3)=2vn
1er terme :v0=u0-3=1-3=-2
raison :q=2
3.Vn=v0qn=(-2)(2)n=-2n+1
4.On pose Sn=v0
+v1+……vn
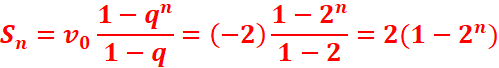
5.![]()
EXERCICE VI :
1.En 1991, on a :P=200 +2%(200)=200+4=204
F
En 1992, on a :P=204
+2%(204)=204+4,08=208,08 F
En 199, on a :P=2088+
2%(208,08)=208,08+4,16=212,24 F
2.Pn=Pn-1 +2%(Pn-1)= Pn-1 +0,02Pn-1=1,02Pn-1.
Pn=1,02Pn-1 <=> Pn+1=1,02Pn => Pn
est une suite géométrique de raison 1,02 et de premier terme 200.
Pn=P0qn=200(1.02)n
3. En 2010, n=2010-1990=20
Pn=P0qn=200(1.02)20=297,189
F