MOUVEMENT D’UN SATELLITE DANS LE CHAMP DE GRAVITATION TERRESTRE
Les
satellites artificiels évoluent dans le champ gravitationnel terrestre. Nombre d’entre
eux ont des trajectoires circulaires dont le centre est le centre de la terre.
Le référentiel galiléen approprié de ce type de mobile est donc le référentiel
géocentrique.
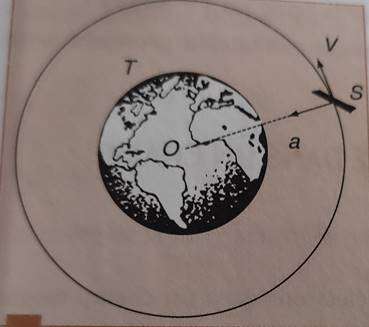
Considérons un
satellite (S) de masse m, évoluant sur une orbite circulaire à une altitude h
au- dessus de la surface de la terre.
Accélération
du satellite
Bilan des forces
Force gravitationnelle
exercée par la terre.
D’après le TCI
=>
a
Le mouvement d’un
satellite est indépendant de la masse ; il ne dépend que du champ de
pesanteur et des conditions initiales de propulsion du satellite.
Vitesse et période de révolution
Vitesse linéaire
=
Période
La période augmente avec l’altitude, elle doit être mesurée dans
un référentiel géocentrique.
EXERCICES
EXERCICE I :
Un satellite d’une tonne tourne autour
de la Terre à une altitude de 1000 km. (Rayon de la Terre ≈ 6370 km,
masse de la Terre ≈ 5,97.1024 kg)
a. Quelle est l’intensité de la
force centripète exercée sur le satellite ?
b. Quelle est son accélération ?
c. Quelle est sa vitesse ?
EXERCICE II :
1-
Un
satellite décrit autour de la terre une orbite circulaire, à une altitude h, à
la vitesse constante v=7x103m.s-1. Calculer h ainsi que
la durée T d’une révolution.
(on
donne RT =6400km; go=9,8ms-2)
2-
Quand
dit-on qu’un satellite est géostationnaire ? A quelle distance h’ doit
graviter le satellite précédant pour être géostationnaire ?
On donne la durée du
jour sidéral : 86164s
3-
L’énergie
potentielle de gravitation du système (Satellite-Terre) s’écrit :
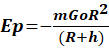
où m est la masse du
satellite
3.1-Quelle est
l’altitude de référence de Ep ?
3.2-Déterminer
l’expression de l’énergie mécanique totale du système (satellite-terre) en
fonction de m, go, R et h.
3.3-Calculer l’énergie
à fournir au satellite pour le faire passer de l’orbite d’altitude h à l’orbite
d’altitude h’. On donne m= 1,5 tonne.
EXERCICE
III :
Situation
problème
Au cours d’un concours scientifique, deux tâches sont proposées à chaque groupe
de deux candidats. Lors du passage du groupe constitué de AKONO et BENJl, les tâches suivantes leur sont proposés : '
Tâche 1
Il leur est demandé d’identifier le satellite géostationnaire parmi les quatre
ci-après.
Après un
travail individuel, les deux sont en désaccord sur la réponse à donner.
Sur le satellite
• Orbite circulaire et vitesse constante.
• L'orbite géostationnaire est une orbite située à 35786 km d’altitude dans le
plan équatorial.
• Expression de la vitesse du satellite : 
=
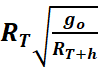
Rayon de la Terre RT=6371km
Intensité du champ gravitationnel sur la surface de la terre g0=9,8m/s2.
En exploitant tes informations ci-dessus et à l'aide d'une démarche
scientifique,
1. Départage AKONO et BENJI sur le satellite qui correspond.
2. Aide les deux candidats à choisir le bon résultat. (
BACCALAUREAT D 2024 extrait)
CORRIGES :
EXERCICE
I :
a.
La force centripète qui
maintient les satellites et planètes sur leurs orbites est la force de
gravitation :
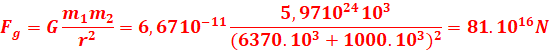
b.
a
c. sa vitesse
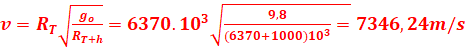
EXERCICE
II :
1-
<= >v2=R2T (g0/RT
+h)
<= >v2(RT
+h)=R2Tg0
<=> v2h+ v2RT=g0
=>h= R2Tg0 /v2-
RT
=(6400
)2x9,8/(7000)2 -6400=1,8.106m
T=2πr/v=2π(RT+h)/v
=2π(6400-1,8.106)/7000=7,35.103 s
2-
Un satellite
est dit géostationnaire lorsqu’il conserve une direction fixe par rapport a un point de la surface de la terre. Un satellite
géostationnaire se déplace donc dans le même sens et a la même vitesse que la
terre autour de l’axe des pôles.
<= >4π2(RT+h’)3/g0R2T=T2
<= >4π2(RT+h’)3 = T2 g0R2T
<=
> 
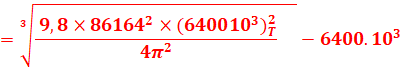
=3,58.107m
3.
3.1-L’énergie
potentielle de gravitation est inversement proportionnelle à l’altitude h, elle
est donc nulle lorsque l’altitude est infinie. La référence des énergies
potentielles est donc prise à une position très éloignée de la terre.
3.2-L’expression
de l’énergie mécanique totale du système (satellite-terre) est :
Em =-Epp +Ec
=-mg0R2T/(RT+h)+1/2mv2
=-mg0R2T/(RT+h)+1/2m
g0R2T/(RT+h)
=-1/2m g0R2T/(RT+h)
3.3-A l’orbite h, l’énergie
mécanique du système est :
Em(h)= -1/2m g0R2T/(RT+h)
A l’altitude géostationnaire, l’énergie mécanique du système
est :
Em(h)=
-1/2m g0R2T/(RT+h’)
La variation d’énergie mécanique est :
ΔEm=Em(h’)-
Em(h)
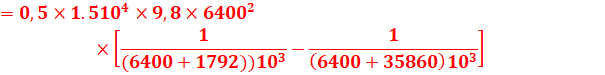
Cette énergie, positive, est l’énergie à fournir pour qu’il passe de
l’orbite d’altitude h à l’orbite géostationnaire.
EXERCICE III :
. Il
s'agit de déterminer la vitesse linéaire d'un satellite géostationnaire afin de
se prononcer.
Pour cela, nous allons :
(i) Utiliser l’expression de la vitesse d'un satellite (donnée) pour calculer
la vitesse d'un satellite géostationnaire ;
(ii) Comparer la valeur obtenue aux valeurs du tableau et conclure.
Vitesse d’un satellite géostationnaire :
=
AN : V≈3072m.s−1
Comparaison et conclusion
La valeur obtenue est égale à celle du satellite S4. Ainsi
c'est S4 qui est un satellite géostationnaire.