SUITES NUMERIQUES

GENERALITES SUR LES SUITES

Définition :

            Une suite numérique (un) est une application de IN dans IR.

(un) : IN→IR

     n→un

On note (un) la suite de nombres u0, u1, u2,..., un, ...

Le nombre un est le terme d’indice n (ou de rang n).

 uo est le premier terme de la suite.

 

On distingue deux types de définition des suites numériques :

Suites définies par une formule explicite

Ce sont des suites dont l’expression directe est en fonction de l’entier n.

Exemple : Un=2n +1

Calculons les 5 premiers termes

U0=2x0 +1=1

U1=2x1 +1=3

U2=2x2 +1=5

U3=2x3 +1=7

U0=2x4 +1=1

 

Suites définies par une formule implicite ou par récurrence

Ce sont des suites définies par la valeur du premier terme et une relation un+1=f(un) pour tout n. Elles sont définies par une formule de récurrence (Formule de récurrence : un terme de la suite s’écrit en fonction du ou des précédents).

.

Exemple : un+1 = 3un + 2 et uo=1

Calculons les deux premiers termes :

u1 = 3u0 + 2= 3x1 + 2=5

u2 = 3u1 + 2= 3x5 + 2=17

 

Le raisonnement par récurrence

Le raisonnement par récurrence permet de montrer qu’une propriété, qui dépend d’un entier naturel est vraie pour tout entier supérieur ou égal à un entier naturel donné.

 Ø Principe de raisonnement par récurrence :

Pour démontrer par récurrence qu’une proposition est vraie pour tout entier naturel (étant un entier naturel donné), on peut suivre les étapes suivantes :

 ·1ère étape : initialisation : On vérifie que la propriété est vraie pour le premier terme. 

· 2ème étape : hérédité : On suppose qu’elle est vraie pour un certain rang p (cette supposition est appelée hypothèse de récurrence), on montre par la suite qu’elle est aussi vraie au rang p+1(on dit dans ce cas que la propriété est héréditaire).

 · 3ème étape : conclusion : Une fois les étapes 2 et 3 sont vérifiées, on conclut d’après le principe de raisonnement par récurrence

qu’elle est vraie pour tout entier naturel.

 

Exemple :

Soit la suite u0=2 et un+1=5un +4, montrons qu’elle est à termes positifs.

·         Initialisation : on montre que le premier terme est positif : u0=2>0

·         Hérédité : on montre que si up>0 alors up+1>0  up+1=5up+4>0 et il y a hérédité.

·         Conclusion : Par récurrence la propriété est vraie pour tout n.

ETUDE D’UNE SUITE NUMERIQUE

Variations d’une suite

Définition :

            Soit (un) une suite de nombre réels. E est son ensemble de définition et I, un intervalle de E.

·         La suite (un) est croissante si, pour tout entier naturel n, un+1 ≥un.

·         La suite (un) est strictement croissante si, pour tout entier naturel n, un+1 > un.

·         La suite (un) est décroissante si, pour tout entier naturel n, un+1 ≤ un.

·         La suite (un) est strictement décroissante si, pour tout entier naturel n, un+1 < un.

Méthode :

a) La méthode algébrique

Ø  On étudie le signe de un+1-un

·         Si pour tout n de E, un+1-un ≥ 0, alors la suite un est croissante.

·         Si pour tout n de E, un+1-un ≤ 0, alors la suite un est décroissante.

Exemple :

Ø   Un compare le quotient             à 1, si pour tout entier naturel n de E, un ≥ 1

 

·   Si pour tout n de E,      alors la suite un est croissante.

 

·   Si pour tout n de E,      alors la suite un est décroissante.

Exemple :

b) Étude à l‘aide d’une fonction

Si un =f(n), alors un a le même sens de variation que la fonction f.

On étudie donc les variations de la fonction sur I contenant E.

·         Si f est croissante sur I, alors la suite un est croissante.

·         Si f est décroissante sur I, alors la suite un est décroissante.

Exemple :

c) Utilisation du raisonnement par récurrence (vu plus haut)

 Suites majorées, minorées, bornées

 Définition :

Soit (un) une suite de nombre réels.

·         La suite (un) est majorée s’il existe un nombre réel M tel que, pour tout entier naturel n, un≤ M.

·         La suite (un) est minorée s’il existe un nombre réel m tel que, pour tout entier naturel n, un≥ m.

·         La suite (un) est bornée si elle est à la fois majorée et minorée.

Exemple :

 Convergence d’une suite

 Définition :

Une suite (un) est une suite convergente vers le nombre réel l si tout intervalle ouvert contenant l contient tous les termes de la suite à partir d'un certain rang. Le nombre réel l est la limite de la suite (un), on écrit :

 

 

Une suite est divergente si elle n’est pas convergente (sa limite est infinie ou n’existe pas).

Théorème : Toute suite croissante et majorée converge. Toute suite décroissante et minorée converge.

Remarque :

Si la suite (un) est croissante et majorée par un réel M, alors la limite de (un) est inférieure ou égale à M; cette limite n'est pas nécessairement M.

 

Suites monotones convergentes :

Théorème : Toute suite croissante et majorée converge. Toute suite décroissante et minorée converge.

Remarque :

Si la suite (un) est croissante et majorée par un réel M, alors la limite de (un) est inférieure ou égale à M; cette limite n'est pas nécessairement M.

Exemple: La suite (un) définie par     et u0 = 0 est croissante et majorée par 2; elle converge donc mais sa limite n'est pas 2 mais le nombre   

Propriétés :

Si (un) converge vers l, et si (un) est croissante, alors pour tout n de IN, un ≤ l. Si (un) converge vers l, et si (un) est décroissante, alors pour tout n de IN, un≥ l.

Suites adjacentes

Définition :

On dit que deux suites (un) et (vn) définies sur IN sont adjacentes si et seulement si les trois conditions suivantes sont réalisées :

 Pour tout entier naturel n, 

Ø  

 

Ø ;

 

Ø

 

 

Théorème :

Si les deux suites (un) et (vn) sont adjacentes, alors elles convergent vers la même limite.

 

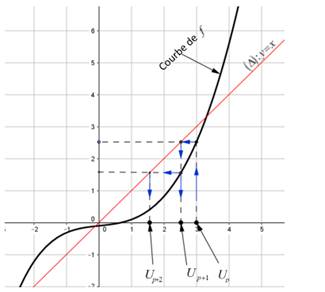
REPRESENTATION GRAPHIQUE DES TERMES D’UNE SUITE

           Si la suite (un) a son terme général défini en fonction de n, on représente la suite dans un repère du plan, par un ensemble de points de coordonnées (n; un). Cette représentation graphique permet de visualiser les variations de la suite et éventuellement la convergence.

 

Méthode :

·         Commencer par représenter la fonction et la première bissectrice.

·         Placer le point d’abscisse u0 sur l’axe des abscisses

·         A partir du point d’abscisse u0 sur l’axe des abscisses, on obtient sur l’axe le point d’abscisse u1 en traçant une parallèle à l’axe des ordonnées qui coupe la courbe au point A0(u0, u1), on trace ensuite une parallèle à l’axe des abscisses qui passe par A0 ; cette parallèle coupe la première bissectrice en un autre point. En traçant une autre parallèle à l’axe des ordonnées passant par ce point, cette nouvelle parallèle coupe l’axe des abscisses au point u1.

·         On répète le processus.

 

 

EXERCICES

EXERCICE I : 

1.Montrer que la suite numérique (un) définie par :   est majorée par 1 et minorée par 0

2.Soit la suite numérique (un) telle que :

 

Montrer par récurrence que pour tout n, 0<un<1.

3.Montrer par récurrence que pour tout n, un= (-4)n+1 +1

 

EXERCICE II :

 

Soit la suite (un) définie par :

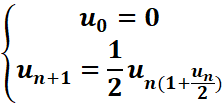
On suppose que la suite (un) est décroissante et que : 0≤un≤1

Démontrer que la suite(un) est convergente et déterminer sa limite.

 

EXERCICE III :

 On considère la suite vn définie par :

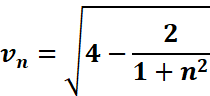
Démontrer que la suite vn est minorée par Ѵ2 et majorée par 2.

 

 

EXERCICE IV :

              Soit la suite (un) telle que  pour tout entier naturel n .

 A - Approche « récurrente » :

1/ Vérifier 0 £ un £ 1 pour tout entier n .

2/ Montrer que la suite u est croissante. Qu’en conclure ?

3/ Calculer  .

 B - Approche « fonctionnelle » :

 Soit f définie sur [0 ; +∞ [ telle que .

1/ Montrer que f est continue, strictement croissante sur [0 ; +∞[

2/ Calculer  

3/ Expliquer pourquoi l’approche « fonctionnelle » permet d’obtenir les résultats cherchés dans la partie A , alors qu’elle n’aurait pas été applicable si on avait définie u par

 .

 

EXERCICE V :

                On considère la suite (un) définie par u0=1 et la relation de récurrence :

 

1) Justifier l’existence de cette suite.

2) Si la suite était convergente, quelle serait sa limite ? Quelle conclusion peut-on en tirer sur le comportement de la suite à l’infini.

 

EXERCICE VI : Soit la suite (un) définie par :

 

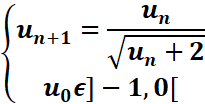
1.Montrer que -1<un<0 pour tout n ϵN

2.Montrer que un est une suite strictement croissante.

3. Montrer que :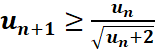

En déduire que :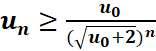

 

CORRIGES

EXERCICE I : 

1.

  

 

 

0 =>

 

2.Soit la suite numérique (un) telle que :

 

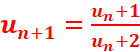
Montrons par récurrence que pour tout n, 0<un<1.

Initialisation :

La propriété est vraie au rang 0, il y a donc initialisation.

hérédité : Supposons la propriété vraie au rang p   c.-à-d     

Montrons qu’alors, la propriété est vraie au rang    p+1    c.-à-d.

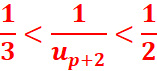
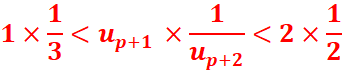
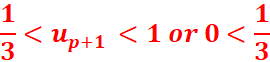
Conclusion : Il y a initialisation et hérédité par récurrence, la propriété est vraie pour tout n.

 

3.Montrons par récurrence que pour tout n, un= (-4)n+1 +1

Initialisation :

La propriété est vraie au rang 0, il y a donc initialisation.

hérédité : Supposons la propriété vraie au rang p   c.-à-d   

Montrons qu’alors, la propriété est vraie au rang    p+1    c.-à-d.

Il y a hérédité

Conclusion : Il y a initialisation et hérédité par récurrence, la propriété est vraie pour tout n.

 

 

EXERCICE II :

La suite (un)  est décroissante et minorée par 0 ;donc elle converge.

On a : 

La fonction f est continue sur [0,1] et pour tout n ϵN, un ϵ [0,1] ; donc la limite de la suite (un) est solution de l’équation : x ϵ [0,1],  f(x)=x

ou x=2

Puisque,0 ϵ [0,1] et 2 non, donc 0 est l’unique solution de l’équation f(x)=x, par suite,

 

 

EXERCICE III :

 

 

 

EXERCICE IV :

 

EXERCICE V :

 

EXERCICE VI :

1.Montrons par récurrence que -1<un<0.

Initialisation :n=0 on a :-1<u0<0

Donc la proposition est vraie pour n=0.

hérédité : supposons la propriété vraie pour n c.-à-d   -1<un<0

montrons qu’elle est également vraie au rang n+1 c.-à-d.  -1<un+1<0.

 

-1<un<0 <=>1<un +2<+2

            <=>1< <

            <=><<1

Et puisque-1<un<0 donc <<1

Donc    <<0   donc  -1<un+1<0.

D’où -1<un<0

2.Montrons que un est strictement croissante.

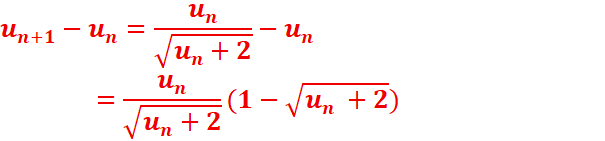
Et puisque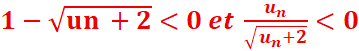

Alors

3. Montrons que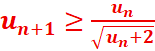

Soit nϵN on a : un≥u0 car un est croissante donc :

 

 c.-à-d   

Donc :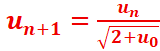

Soit n ϵN on a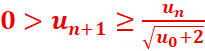

Donc :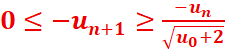

En donnant les valeurs a n , on trouve :

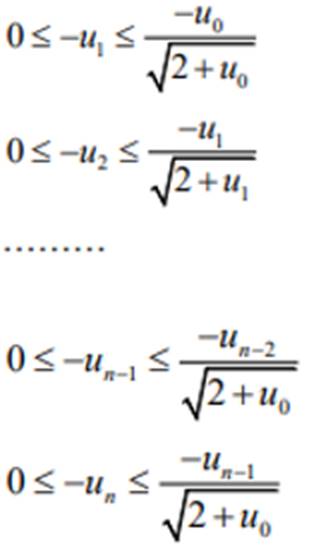
Le produit des inégalités donne :

 

 

 

 

 

 

 

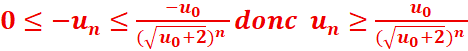
Merci de votre visite
Laissez un commentaire