MOUVEMENT D’UN VEHICULE DANS UN VIRAGE
Considérons le mouvement d’un cycliste qui
aborde un virage circulaire de rayon r.
Dans
le référentiel terrestre, supposé galiléen, les forces appliquées au système
formé par le cycliste et sa bicyclette sont, en l’absence des forces de
frottements :
-la
réaction 
de la piste.
-
le poids 
de l’ensemble.
D’après
le TCI
Le
cycliste ne peut prendre le virage que si la résultante des forces sui lui sont
appliquées est centripète (dirigée vers le centre de la trajectoire). Ceci
n’est possible que lorsque la piste est inclinée par rapport à l’horizontale ou
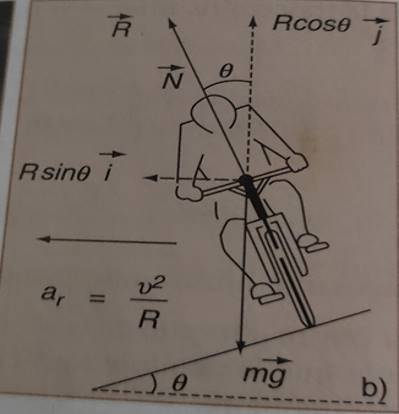
lorsqu’il existe des frottements. Si θ est l’angle d’inclinaison de la
piste, les projections de la relation précédente dans le repère (G,I,J) lié au mobile
et choisi tel que (G,I) soit horizontal dans la direction du rayon r de la trajectoire et (G,J) vertical sont :
Rsinθ = m
(1)
Rcosθ = mg (2)
La
force centripète ici est attribuable à la composante horizontale Rsinθ de
la réaction.
Des
relations (1) et (2), on tire :
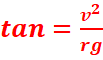
L’angle
d’inclinaison de la courbe d’une route qui permet à un véhicule de prendre un
virage sans déraper, en l’absence des frottements ne dépend que de la vitesse v
du véhicule et du rayon de courbure r du virage.
EXERCICES
EXERCICE
I :
Une
automobile de 1000 kg aborde un virage relevé d’un angle de 30 degrés par
rapport à l’horizontale. On donne le rayon du virage : 100 m 1. 1.Déterminer la
vitesse maximale sans risque de dérapage en l’absence des frottements ?
2.Determiner la réaction de la piste
EXERCICE
II :
Pour bien concevoir un virage, l’ingénieur doit
connaitre son rayon de courbure et la valeur de la vitesse prévue pour aborder
ce virage. Un virage de rayon de
courbure 50m a été relevé de 14 degrés.
1.Un
véhicule de1400kg abordant ce virage à la vitesse de 60 km/h risque-il un
dérapage ?
2.
Quelle serait la force de frottement nécessaire pour aborder ce virage à cette
vitesse sans déraper s’il n’était pas relevé ?
EXERCICE III :
Dans
un virage de 50 m de rayon, on a relevé le bord extérieur d’une piste de course
afin que la chaussée fasse un angle de 20 degrés avec l’horizontale. On désire
calculer le module maximal de la vitesse à laquelle une voiture de 1200kg peut
négocier le virage sans déraper. Il y a un coefficient de frottement statique
de 0,8 entre les pneus et la chaussée.
On rappelle que la force de frottement est
proportionnelle à la réaction normale f=μn ou μ est le coefficient de
frottement statique
1.
Calculer
la réaction normale n.
2.
Déterminer
la vitesse maximale de cette voiture sans risque de dérapage.
EXERCICE IV :
Situation problème
ABDOULAYE voyage avec sa voiture de puissance P=50ch et de
masse m sur un axe qui a plusieurs phases.
Phase 1 : Il grimpe une colline rectiligne de pente 20% (sinθ=0,2) à
vitesse constante, le moteur tournant en plein régime (P=50ch). Sur cette
montée, il traverse une plaque délimitation de vitesse (vitesse maximale
50km/h) où est placée une équipe de contrôle de gendarmerie qui l'interpelle et
lui impose le payement d'une amende de 25000 Fcfa pour dépassement de la
vitesse autorisée.
Phase 2 : Quelques kilomètres plus loin, il aborde un virage avec la vitesse V
= 50 km/h (voir figure ci-dessous) et dérape.
Hypothèse : Sur cet axe, les forces de frottement de la route sont
négligeables.
Données : α=5,0o; r=150m ; g=9,8N/kg,
m = 1,0 tonnes ; 1 ch = 736 W
En exploitant les informations ci-dessus et en utilisant une démarche
scientifique ;
1. Examine si le chauffeur du-véhicule mérite d'être verbalisé. 4pts
2. Explique la cause du dérapage du véhicule. 4pts
CORRIGES
EXERCICE I :
1.En
l’absence des frottements, on a :
2. Rcosθ = mg => R=mg/cosθ=1000x10/cos30=11547N.
EXERCICE II :
1.Un véhicule abordant ce virage à la vitesse de 60 km/h risque-il
un dérapage.
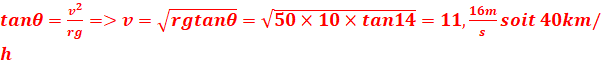
Il risque un dérapage en l’absence des frottements car 60>40.
2. Quelle serait la force de frottement nécessaire pour aborder ce
virage sans déraper s’il n’était pas relevé ?
Soit f la
force de frottement,
f=mv2/r=1400(16,66)2/50=7772N
EXERCICE III :
1.Calculer de
n.
D’après le
TCI,
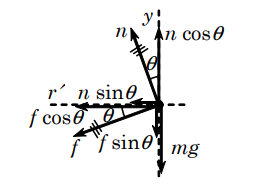
Projection sur l’axe des y :
-mg -fsinθ +ncosθ =0
<=>-mg-μnsinθ+ ncosθ =0
<=>n(cosθ -μsinθ)=mg
=>n=mg/(cosθ -μsinθ)
=1200x10/(cos20 -0,8sin20=17656N
2.Déterminer la
vitesse maximale sans déraper
Projection
sur l’axe des x(r’) :
fcosθ+nsinθ=mv2/r
=>v2=r(fcosθ+nsinθ)/m= rn(μcosθ+sinθ)/m
=50x17656(0,8cos20+sin20)/1200=804,65
v=Ѵ804,65=28,36m/s
EXERCICE IV :
Il s’agit de trouver la vitesse du véhicule afin de voir si le chauffeur
mérite d'être verbalisé.
Pour cela il faut :
• Établir le bilan des forces appliquées au véhicule ;
• Utiliser le principe de l’inertie pour déterminer l’intensité de la force
motrice du véhicule :
• Utiliser l’expression de la- puissance instantanée pour déterminer la vitesse
du véhicule
• La comparer à la valeur de la plaque de limitation de vitesse et conclure.
1.1. Bilan des forces
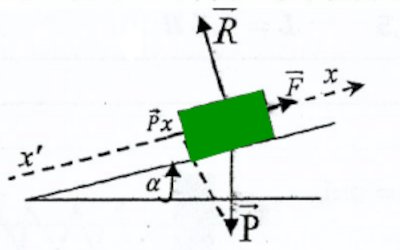
1.2.Détermination
de l’intensité de la force motrice F.
Projection suivant suivant l’axe x’x
F=mgsinα
La puissance développée par le moteur de la voiture est donnée par :
P= FVcos(
) or c cos() =1 car () =0
V=PF=Pmgsinθ
AN : V=18,77 m/s = 67,59 km/h
1.4. Comparaison :
Finalement V≻50km/h
Conclusion : le chauffeur doit être verbalisé.
2. il s'agit de trouver la
vitesse limite pour que le véhicule prenne ce virage afin d’expliquer la cause
du dérapage.
Pour cela il faut:
• Établir le bilan des forces appliquées au véhicule;
• Utiliser le TCI pour déterminer cette vitesse;
• La comparer à la vitesse du véhicule lors de la prise du virage et conclure.
2.1. Bilan des forces
2.2.Détermination
de la vitesse limite pour que le véhicule prenne le virage
D’après le TCI, 
Utiliser le triangle dynamique, nous
avons tanα=maGmg or aG=V2maxr
en remplaçant aG par son expression on obtient
: tanα=V2maxgr⇒ Vmax=√rgtanα
Vmax=40,8 km/h
2.3. Comparaison :
Pour prendre le virage sans déraper, Vmflï = 40,8 km/h
0n constate que V≻Vmax
Conclusion : Le véhicule dérape parce que sa vitesse est supérieure à la
vitesse limite prévue pour prendre le virage.