SIMILITUDES

DEFINITIONS 

· On appelle similitude plane toute application f du plan dans lui-même telle que :

∃k ∈ R ^∗ +, ∀ M, N ∈ P, d’images respectives M’et N’

M’N’= kMN.

k est le rapport de la similitude s.

· Une similitude directe plane est une similitude plane f qui conserve l’orientation des angles.

· On appelle similitude indirecte de rapport k toute similitude qui ne conserve pas l’orientation des angles.

· Une isométrie est une application qui conserve les distances.

· On appelle déplacement une translation ou une rotation.

SIMILITUDES DIRECTES DU PLAN

Ø Toute similitude directe de rapport k est :

-soit une translation

-soit une rotation

-soit une homothétie de rapport k

-soit la composée d’une rotation et d’une homothétie de rapport k.

Ø Toute similitude directe de rapport k est aussi la composée d’une homothétie de centre O et de rapport k, d’une rotation de centre O et d’une translation.

Propriété 1.

Une similitude directe est la composée d’un déplacement et d’une homothétie.

Propriété 2 :

On peut vérifier facilement que :

1) Toute translation, toute homothétie et toute rotation est une similitude directe.

2) L’identité est une similitude.

3) Une isométrie est une similitude de rapport 1.

4) La composée de deux similitudes de rapports respectifs k₁ et k₂ est une similitude de rapport k₁ × k₂ .

5) La réciproque d’une similitude de rapport k est une similitude de rapport 1/ k .

6) Toute similitude de rapport k est la composée d’une homothétie de rapport k et d’une isométrie.

Propriété 3 :

Dans une similitude de rapport k, le produit scalaire est multiplié par k ² .

Propriété 4 :

Une similitude conserve les angles géométriques.

Propriété 5 :

Un repère orthogonal se transforme par une similitude en un repère orthogonal, c’est à dire qu’un triangle rectangle isocèle se transforme en un triangle rectangle isocèle.

Propriété 6 :

Une similitude transforme une droite en droite, un cercle en cercle.

Propriété 7 :

Une similitude conserve les angles géométriques, le parallélisme, l’orthogonalité, l’alignement, le contact, le barycentre et multiplie les aires par le carré de son rapport.

Exemple :

On donne un triangle équilatéral direct ABC du plan orienté. On note I le milieu de [BC]. On considère la similitude directe s telle que : s(I) = B et s(B) = A. Déterminons le rapport et l'angle de s.

Soit k le rapport de s et θ son angle.

s(I) =B et s(B)= A <= >BA=kIB et mes (𝐼𝐵⃗, 𝐵𝐴⃗) =θ

k= BA/IB=2IB/IB=2

Le triangle est équilatéral direct : θ=-2π/3

Donc s est une similitude directe de rapport 2 et d’angle - 2 π/3

SIMILITUDES DIRECTES ET NOMBRES COMPLEXES

Ecriture complexe d’une similitude plane directe

Le plan complexe est rapporté à un repère orthonormé direct (O;⃗𝑢 ;⃗𝑣 ).

Définition

Une similitude directe est une transformation du plan dont l’écriture complexe est de la forme :

z’=az + b où a ∈ ℂ* et b ∈ ℂ.

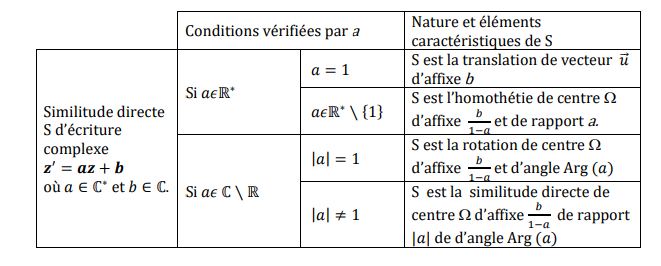
Propriété

Soit s une similitude directe d'écriture complexe z' = a z + b où a ∈ ℂ* et b ∈ ℂ.

* Si a =1, alors s est la translation de vecteur d'affixe b.

* Si a ≠1 alors s est la similitude directe de centre d'affixe 𝑏 /1−𝑎 , de rapport |a|, d'angle arg(a).

La similitude s admet un seul point fixe Ω. Cette similitude est alors la composée dans un ordre indifférent d’une homothétie de rapport k = |a| de centre Ω et d’une rotation de même centre et d’angle θ = arg(a). Si ω est l’affixe de Ω, on a alors :

z’ − ω = ke^iθ (z − ω)

NB : Lorsque 𝑎 ≠ 1, la similitude directe est caractérisée par : son centre, son rapport et son angle.

Détermination des caractéristiques d’une similitude directe donnée connaissant son ecriture complexe.

Méthode.

Pour déterminer les équations caractéristiques d’une similitude directe s d’expression complexe z’= az + b (a ∈ C ∗\{1}, b ∈ C),

1. Résoudre l’équation z = az + b, on obtient le centre de s.

2. Calculer le module de a, on obtient le rapport de s.

3. Déterminer un argument de s, on obtient l’angle de s.

Exemple1 :

Déterminons les éléments caractéristiques de la similitude directe S dont l’écriture complexe est : 𝑧 ′ = (1 − 𝑖)𝑧 + 𝑖

Solution

L’écriture complexe de S est de la forme

𝑧 ′ = 𝑎𝑧 + 𝑏 où a = 1 – i, et b = i.

a ≠1. Soit A le centre de S, k son rapport et θ son angle.

• L’affixe du centre A est

𝑏 /1−𝑎 = 𝑖 /1−(1−𝑖) = 𝑖/ 𝑖 =1

• Le rapport k est tel que : k = |a| ,

=> k = √2

• L’angle q est tel que : θ= Arg(a)

On a : cosθ = √2/ 2 et sinθ = − √2 /2 , donc θ = − π /4

S est la similitude directe de centre A d’affixe1, de rapport √2 et d’angle − π/ 4

Exemple2 : On donne une similitude s dont l’ecriture complexe est

z=(1 − i √ 3)z − 1 + i

Cherchons le rapport et le centre

Solution :

L’écriture complexe de la transformation f est de la forme

z’ = az + b, donc f est une similitude directe.

Si Ω est le centre, ce point est invariant : f(Ω)=Ω

<=>z = (1 − i √ 3)z − 1 + i

=> ω = −1 + i /1 − 1 + i √ 3

= −1 + i/ i √ 3 = 1 + i/ √ 3

= 1 /√ 3 + i /√ 3 .

De plus, (1 + i √ 3) = 2( 1/ 2 − i √ 3 /2 ) = 2e ^{−i π /3} .

On en déduit que f est une similitude directe de centre Ω(1/√3 ; 1/√3) de rapport 2 et d’angle − π /3.

Remarque

• Toute rotation de centre A et d’angle a est une similitude directe de centre A , de rapport 1 et d’angle a.

•Toute homothétie de centre A et de rapport k (𝑘 > 0) est une similitude directe de centre A, de rapport k et d’angle nul.

•Toute homothétie de centre A et de rapport k (𝑘 < 0) est une similitude directe de centre A , de rapport −𝑘 et d’angle 𝜋. .

Détermination de l’écriture complexe d’une similitude directe donnée par son centre, son rapport et son angle.

Le plan complexe est rapporté à un repère orthonormé direct (O, u, 𝑣).

Propriété

Soit M’un point du plan d'affixe z' qui est l’image d'un point M d'affixe z par une similitude directe S de centre W d’affixe 𝑧W , de rapport k et d'angle q. On a : z’ − ω = ke^iθ (z − ω)

Exemple : Donnons l’expression complexe de la similitude s de centre Ω(2; −1) de rapport 2 et d’angle π/ 6 .

Solution.

La similitude directe s a pour point invariant Ω d’affixe ω = 2 − i.

On a : z’= az + b ⇒ω = aω + b

⇒b=ω(1 − a)

⇒ z’= az ω(1 − a)

⇒ z’ = az + ω(1 − a).

Donc

z’= 2e ^{i π /6} (z − 2 + i) + 2 − i

= 2( √ 3 2 + i 2 )(z − 2 + i)) + 2 − i

= (√ 3 + i)(z − 2 + i) + 2 − i

= (√ 3 + i)z − 2 √ 3 − 1 − 2i + i √ 3 + 2 − i

= (√ 3 + i)z + 1 − 2 √ 3 + i( √ 3 − 3).

Images de figures simples par une similitude directe

Propriété 1

Toute similitude directe de rapport k transforme :

• une droite en une droite ;

• une demi-droite en une demi-droite ;

• un segment de longueur ℓ en un segment de longueur kℓ ;

•un cercle de centre A et de rayon 𝑟 en un cercle de centre A’, image de A par la similitude directe, et de rayon 𝑘𝑟.

Propriété 2

Toute similitude directe de rapport 𝑘 multiplie :

• les distances par 𝑘 ;

• les aires par 𝑘²

Expression analytique d’une similitude directe plane

Soit f est une similitude directe d’expression complexe z’= az + b.

Posons z = x + iy, z’ = x’+iy’, a = α + iβ et b = m + in avec x, x’ , y, y’ , α, β, m, n ∈ R.

z’= az + b ⇐⇒ x’ + iy’ = (α + iβ)(x + iy) + m + in

⇐⇒ x’ + iy’ = α(x + iy) + iβ(x + iy) + m + in

⇐⇒ x’ + iy’ = αx + iαy + iβx − βy + m + in

⇐⇒ x’ + iy’ = αx − βy + m + i(αy + βx + n)

⇐⇒

Le système obtenu est l’expression analytique de la similitude directe f.

Exemple.

1.Déterminer l’expression analytique de la similitude directe s définie par

z’= (1 − 2i)z − 3 + i

2.Déterminer l’expression complexe puis la nature et les éléments caractéristiques de la similitude directe dont l’expression analytique est

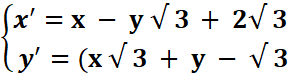
Solution.

1. Posons z = x + iy et z’ = x’+iy’ .

Alors, z’ = x’+iy’= (1 − 2i)(x + iy) − 3 + i

= x + iy − 2ix + 2y − 3 + i

= x + 2y − 3 + i(−2x + y + 1)=>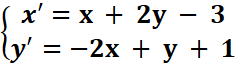

2.

z’=x’+iy’ = x − y √ 3 + 2√ 3 + i(x √ 3 + y − √ 3)

= x(1 + i √ 3) + y(− √ 3 + i) + 2√ 3 − i √ 3

= (z + 𝑧̅)/2 (1 + i √ 3) + (z - 𝑧̅)/ 2i (− √ 3 + i) + 2√ 3 − i √ 3 // On sait que: x=(z+ 𝑧̅)/2 et y=(z- 𝑧̅ )/2i

=[ (1 + i √ 3 )/2 +( − √ 3 + i)/ 2i ]z +[ (1 + i √ 3)/ 2 – (− √ 3 + i)/ 2i ] 𝑧̅ + 2√ 3 − i √ 3 // car 1/2i=-i/2

= (1 + i √ 3)z + 2√ 3 − i √ 3

L’équation z’ = (1 + i √ 3)z + 2√ 3 − i √ 3 a pour unique solution (2 √ 3−i √ 3) /(1−1−i √ 3) = 1 − 2i.

De plus, 1 + i √ 3 = 2( 1 /2 + i √ 3 /2 ) = 2e ^{i π /3} .

Donc f est une similitude directe de centre Ω(1, −2), de rapport k = 2 et d’angle θ = π/ 3.

EXERCICES

EXERCICE I :

On donne trois points A, B et C deux à deux distincts et un point D tels que : 𝐴𝐷⃗ = 2𝐴𝐵⃗ − 5𝐶𝐷⃗.

1.On considère la similitude directe s telle que : s(A) = A', s(B) = B', s(C) = C' et s(D) = D'.

Justifie que : 𝐴⃗’𝐷⃗ ′ = 2𝐴⃗’𝐵⃗′ − 5𝐶⃗′ 𝐷⃗′ .

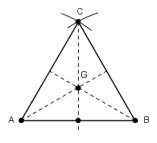
2. ABC est un triangle équilatéral direct de centre de gravité G. I est le milieu de [AB].

Pour chacune des similitudes directes suivantes préciser son rapport et son angle.

a- s₁ a pour centre B et s₁(I) = C

b- s₂ a pour centre I et s₂(A) = C

c- s₃ a pour centre A s₃(G) = C

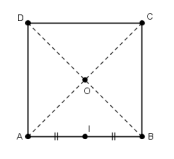
3. ABCD est un carré direct. O est le centre de ABCD et I le milieu de [AB].

Pour chacune des similitudes directes préciser son rapport et son angle.

a- s₁ a pour centre C et s₁(A) = B

b-s₂ a pour centre O et s₂(I) = C

EXERCICE II :

1.Considérons la similitude directe plane définie par z’ = (− 1 /2 + i √ 3 /2 )z + 3 + i √ 3.

Déterminer les éléments caractéristiques de s

2. Déterminer les éléments caractéristiques de la similitude directe d’écriture complexe : z’= (−2 + 2i)z + 5 + i

3.Détermine l’écriture complexe de la similitude directe de centre A d’affixe i, de rapport √2 et d’angle π/4 .

4.On considère les similitudes directes

s₁ : z’= 2iz+1−2i et s₂ : z’= (1−i)z+1+i.

Déterminer l’expression complexe puis la nature et les éléments caractéristiques de le similitude s₂ ◦ s₁ et de s −1 .

EXERCICE III :

Soit s la similitude directe d’écriture complexe : z’ = (1 − i) z + 2 − i.

1. Déterminer les éléments caractéristiques de s.

2. Déterminer et construire l’ensemble des points M d’affixe z tels que :

| (1 − i) z + 2 − i |= 4

3. Retrouver le résultat de la question précédente par une méthode algébrique.

EXERCICE IV :

Le plan complexe est muni d'un repère orthonormé direct.

On considère l'application s du plan dans lui-même qui à tout point M de coordonnées (x, y), associe le point M' de coordonnées (x', y') telles que :

1) Trouve l'écriture complexe de s.

2) Déduis-en que s est une similitude directe.

CORRIGES

EXERCICE I :

1.

//𝐴𝐷⃗ = 2𝐴𝐵⃗− 5𝐶𝐷⃗

Û −6𝐴𝐷⃗ + 2𝐴𝐵⃗ + 5𝐴𝐶⃗ = ⃗0 .

Û A = bar{(D, -6) ; (B, 2) ; (C, 5)}.

Toute similitude directe conserve le barycentre.

D'où, A' = bar{(D', -6) ; (B', 2) ; (C', 5)}.

Donc, −6𝐴⃗′𝐷⃗′ + 2𝐴⃗𝐵⃗ ′ + 5𝐴′𝐶′ ⃗= ⃗0 . Par suite 𝐴′𝐷′ ⃗= 2𝐴′𝐵′ ⃗ − 5𝐶′𝐷′ ⃗

2.

a- s1 a pour centre B et s1(I) = C On obtient alors pour rapport et angle :

s₁(I) = C

s₁(B) = B (point invariant) <= >BC=kBI =>k = BC /BI =2BI/BI= 2 et θ = − π /3

b- s2 a pour centre I et s2(A) = C On obtient alors pour rapport et angle :

s₂(A) = C

s₂(I) = I (point invariant) <= >IC=kIA =>k = IC /IA

IC²=AC²-IA²=(2IA)²-IA²=3IA² =>IC=Ѵ3IA

=>k = IC /IA= Ѵ3IA/ IA=Ѵ3 et θ = - π /2

c- s₃ a pour centre A s3(G) = C On obtient alors pour rapport et angle :

s₃(G) = C

s₃(A) = A (point invariant) <= >AC=kAG =>k = AC /AG

AG=2/3AJ=2/3IC=2/3 X Ѵ3IA=2/3 X Ѵ3XAC/2

=>k = AC /AG=AC/2/3 X Ѵ3XAC/2=√ 3 et θ = π

3.

a- s₁ a pour centre C et s₁(A) = B On obtient

alors pour rapport et angle : k = CB /CA = √ 2 /2 et θ = π /4

b-s₂ a pour centre O et s₂(I) = C On obtient

alors pour rapport et angle : k = OC/ OI = √ 2 et θ = 3π

EXERCICE II :

1.On a : | − 1/ 2 + i √ 3/ 2 | = 1

et arg(− 1/ 2 + i √ 3/ 2 ) = 2π /3 (2π).

D’autre part, 3+i √ 3 /(1+ 1/ 2 −i √ 3/ 2)

= 3+i √ 3 /(3 /2 −i √ 3 /2)

= 2(3+i √ 3)/ (3−i √ 3 }

= 2(3+i √ 3)(3-iѴ3)/( (3+i √ 3)(3-iѴ3)=2

= 2(6+6i √ 3) /12 = 1 + i √ 3.

Cette similitude directe est donc la rotation d’angle θ = 2π /3 et de centre Ω(1; √ 3).

2.On obtient donc :

➪ k = | − 2 + 2i| = 2|1 + i| = 2 √ 2

➪ on a alors cos θ = − 1 /√ 2 et sin θ = 1/ √ 2,

on obtient donc θ = 3π /4

➪ on résout l’équation au point fixe pour obtenir le centre :

ω = (−2 + 2i)ω + 5 + i

< =>ω(1 + 2 − 2i) = 5 + i

< =>ω(3 − 2i) = 5 + i

=>ω =( 5 + i )/(3 − 2i)

= (5 + i)(3 + 2i)/13=1+i

3.

z' = √2𝑒 ^{𝑖 π /4}(z − z_A) + z_A

z'= √2 ( √2 /2 + 𝑖 √2 /2 ) (𝑧 − 𝑖) + 𝑖

z'= (1 + 𝑖)(z – 𝑖) + 𝑖 z'= (1 + 𝑖)z + 1

L’écriture complexe de la similitude directe s est : z'= (1 + 𝑖)z + 1.

4.

s₁ a pour expression complexe

z’ = 2e ^{i π /2} z + 1 − 2i.

Donc elle a pour rapport k₁ = 2 et d’angle θ₁ = π/ 2 .

s₂ a pour expression complexe

z’= √ 2e ^{−i π/ 4} z + 1 + i.

Donc elle a pour rapport k₂ = √ 2 et d’angle θ₂ = − π /4 .

La composée s₂ ◦ s₁ est donc une similitude directe de rapport

k = k₁k₂ = 2√ 2 et d’angle θ = θ₁ + θ₂ = π/ 2 − π /4 = π/ 4 .

La réciproque s₁ ⁻¹ de s₁ est une similitude directe de rapport

k’= 1/ k1 = 1 /2 et d’angle θ’ = −θ₁ = − π/ 2 .

Attention ! ! s ◦ s ₀ et s ₀ ◦ s ne sont pas égales.

Remarque. Si deux similitudes directes ont même centre, alors s ₀ ◦ s = s ◦ s ₀ , c’est-á-dire composées d’homothéties et de rotations de même centre.

EXERCICE III :

1. Soit M(z). On a s(M) = M

⇒ z = (1 − i)z + 2 − i

⇒ [1 − (1 − i)]z = 2 – i

iz = 2 − i =

⇒ z = (2−i)/ i = −1 − 2i.

Par ailleurs 1 − i = √ 2( √ 2/ 2 − i √ 2 /2 ) = √ 2e ^{−i π/ 4} .

Donc s est la similitude de centre

Ω(−1; −2) de rapport √ 2 et d’angle −π/ 4 .

2. On a : |(1 − i)z + 2 − i| = 4

// (1 − i)z + 2 − i =(1-i)[z +(2-i)/1-i]

|(1 − i)z + 2 − i|=|(1-i)[z +(2-i)/1-i]|=|1-i|| z +(2-i)/1-i|

L’équation peut être réécrite sous la forme :

|z- (-2+i)/(1+i)|=4/|1-i|

En simplifiant, on obtient :

⇒ |z + 3+i /2 | = 2√ 2

⇒ AM = 2√ 2 avec A(− 3/ 2 ; − 1/ 2 ). Donc M décrit le cercle C(A; 2√ 2).

3. Retrouvons ce résultat par une méthode algébrique.

Posons z = x + iy et z’= x’ + iy’ .

On a : |(1−i)z+2−i| = 4 =⇒ |(1−i)(x+iy)+2−i| = 4 =⇒ |x+y+2+i(−x+y−1)| = 4 =

⇒ (x+y+2)²+(−x+y−1)² = 16

⇒ x ²+y ²+4+4x+4y+2xy+x ²+y ²+1+2x−2y−2xy = 16 =

⇒ 2x ²+2y ²+6x+2y+5 = 16

⇒ x ²+y ²+3x+y+ 5/ 2 = 8

⇒ (x+ 3/ 2 ) ²− 9/ 4+(y+ 1/ 2 ) ²− 1/ 4+ 5/ 2 = 8 =

⇒ (x + 3/ 2 ) ² + (y + 1/ 2 ) ² = 8.

Donc M décrit C(A; 2√ 2).

9 + 4 = 15 + 10i + 3i – 2/ 13 = 13 + 13i /13 = 1 + i la similitude est de rapport 2√ 2 d’angle θ = 3π/ 4 et de centre Ω(1 + i).

EXERCICE IV :

1)Posons : z = x + iy et z' = x' + iy' ou z et z’ sont les affixes respectives de M et M’.

z = x + iy

z' = x' + iy'

z' = (x +y -3) + i(- x+ y +2) z' = x +y -3 + - ix + i y +2i

= (1- i)x + (1+ i)y - 3 + 2i = (1 - i)x + (1- i)iy - 3 + 2i |

on met i en facteur dans le bloc (1+i)y = (1- i)(x + iy) - 3 + 2i = (1 - i)z - 3 + 2i

L'écriture complexe de S est : z’ = (1 - i)z - 3 + 2i.

2) L'écriture complexe de s est de la forme :

z' = az + b où a Î ℂ* et b Î ℂ.

D'où, s est une similitude directe.

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire